


|
Le modèle présenté ici était prêt, dans ses grandes lignes, en 1992. Dans les années qui ont suivi, plusieurs discussions sur le forum rec.music.early, en particulier avec Margo Schulter à propos de l’accord pythagoricien et Pierre Funck au sujet des ajustements de comma, m’ont permis de l’affiner et de mieux l’expliciter. Mais je n’aurais jamais osé rendre public ce qui suit sans la providentielle rencontre, en été 1998, d’Yves Ouvrard et de Jean-Pierre Vidal qui se sont employés avec enthousiasme à développer l’outil logiciel dont je rêvais, mais que je n’aurais jamais été capable de réaliser seul. Qu’ils trouvent ici l’expression de ma gratitude. |
Dans la deuxième partie de ses Istitutioni Harmoniche1, Gioseffo Zarlino livre ce qui constitue l’une des premières descriptions précises d’un tempérament musical2. A l’issue de cet exposé, il consacre un chapitre à l’intonation vocale, déclarant de manière on ne peut plus claire que les chanteurs a cappella tendent à utiliser non pas un tempérament particulier mais les intervalles dans leur « forme vraie3 ». Cette affirmation fait de lui le prophète4 de ce que des théoriciens ultérieurs ont appelé « intonation juste5 ». Plutôt qu’une démonstration, qu’il n’a guère les moyens de construire, c’est un credo qu’il livre: il pose un idéal6, pas forcément atteint mais néanmoins hautement désirable. Soucieux de s’assurer la caution des anciens, il identifie le système qu’il préconise à l’un de ceux proposés par Ptolémée au deuxième siècle de notre ère. Le nom de ce théoricien de l’Antiquité vient ainsi faire pendant à celui de Pythagore, traditionnellement attaché au seul système en vigueur dans la théorie médiévale.
Alors que, si l’on s’intéresse à l’intonation instrumentale, on peut tirer des renseignements précieux aussi bien des traités techniques que des instruments eux-mêmes ou de tableaux les représentant7, cette profession de foi est, avec la controverse qu’elle a provoquée, notamment entre Zarlino et son ancien élève Vicenzo Galilei8, le seul point de départ dont nous disposions pour aborder l’intonation des chanteurs au xvie siècle.
L’intonation juste a de tout temps été considérée par certains comme une chimère. Ils y voient, peut-être à raison, un caprice de mathématicien sans réel contenu musical. Il n’en demeure pas moins que cette « illusion » a longtemps fait l’objet d’une quête que Haynes n’hésite pas à comparer à celle du Graal9. S’il est un point de l’espace-temps où cette quête avait quelque chance d’aboutir, il se situe à coup sûr dans l’une ou l’autre des cappelle et camerate de très haut niveau qui fleurissent dans l’Italie du xvie siècle, ce microcosme qui voit « tous les praticiens, mus par l’autorité de Zarlino10 », rechercher assidûment la meilleure intonation possible. C’est à cette époque plus qu’à n’importe quelle autre que l’intonation juste a pu faire l’objet d’une pratique plus ou moins consciente et raisonnée.
Seulement, une telle affirmation gagnerait en consistance si l’intonation juste était autre chose qu’une idée vague. Sa mise en pratique implique en effet des choix qui peuvent conduire à des résultats fort divers. C’est en vain qu’on cherche, dans la littérature ancienne ou moderne, un mode d’emploi permettant de l’appliquer à des exemples musicaux concrets. Ce que nous tentons de décrire n’est certainement pas une marche à suivre rigide, c’est avant tout un modèle de référence, dont nous souhaitons, mais ce n’est pas l’essentiel, qu’il puisse avoir aujourd’hui une utilité pratique. Si des chanteurs de la Renaissance ont pratiqué une forme d’intonation juste, quelles ont pu être leurs stratégies, explicites ou implicites, conscientes ou inconscientes pour s’approcher de cet idéal ? Voilà la principale question que nous nous poserons. Nous serons alors amené à nous en poser une autre, plus brûlante à une époque où de nombreux ensembles vocaux se consacrent à la polyphonie de la Renaissance : de quelle manière des chanteurs d’aujourd’hui qui auraient adopté l’idéal de Zarlino peuvent-ils procéder pour l’atteindre ? Nous postulons que ces deux questions ont la même réponse ou, tout au moins, que la réponse à la seconde ne peut faire l’économie d’une réflexion en profondeur à propos de la première.
Un peu oubliée auparavant, l’intonation juste fut remise au goût du jour par le naturalisme de l’époque romantique, et notamment par le grand physicien Helmholtz qui fit accorder un « harmonium juste » pour mener ses expériences. Tout en prônant un usage universel de sa « gamme naturelle » par les chanteurs et les violonistes de son temps, il la juge particulièrement appropriée à la musique de la Renaissance :
Les particularités de la gamme naturelle se manifestent surtout dans l’ancienne musique italienne de Palestrina, Vittoria, Gabrieli et leurs contemporains. Ces œuvres réclament les consonnances les plus justes parce qu’elles n’obtiennent les nuances les plus délicates de l’harmonie que par les renversements des accords, l’alternance des accords majeurs et mineurs, et un petit nombre de dissonances formées par des retards. Exécutées dans la gamme tempérée, elles perdent tout sens et toute expression, tandis que, grâce à l’emploi de la gamme naturelle, elles produisent souvent sur l’harmonium un bon effet11.
Il reconnaît aussi que les chanteurs qu’il a entendus sont pour la plupart incapables de chanter « de manière à donner à l’auditeur ce bien-être complet qui résulte d’une parfaite harmonie », ce qu’il attribue à l’influence néfaste des pianos accordés au tempérament égal avec lesquels ils s’exercent. Les choses étaient bien différentes par le passé :
Jusqu’au dix-septième siècle, les chanteurs étaient enseignés au moyen du monochorde pour lequel Zarlino, au milieu du seizième siècle, avait retrouvé la vraie gamme naturelle12.
Mais quelle est donc cette « vraie gamme naturelle » dont Zarlino doit, bien malgré lui, assumer la paternité ? Sans entrer dans le détail de la discussion de Helmholtz, qui s’appuie notamment sur une nomenclature modale très personnelle, on l’identifiera à ce qu’il appelle « gamme majeure » et qu’il décrit par les rapports de fréquences suivants13 :
ut1 - ré - mi - fa1 - sol - la - si - ut2
1 - 9/8 - 5/4 - 4/3 - 3/2 - 5/3 - 15/8 - 2
C’est cette gamme qui, reprise à l’infini dans des dizaines d’ouvrages théoriques plus ou moins récents, sous des noms divers comme gamme de Zarlino, gamme naturelle ou gamme des physiciens, a fondé un certain nombre de jugements définitifs tant sur l’intonation juste que sur Zarlino lui-même. Que faut-il en penser ? Avant tout qu’il s’agit d’un anachronisme grossier : quoi que puisse laisser penser l’examen superficiel d’une figure (Figure 1.1) apparaissant dans son traité, Zarlino n’a pu en aucune manière « retrouver la gamme naturelle », pour la simple et bonne raison que la notion de gamme et celle, corollaire, de tonalité, n’existaient pas à la Renaissance. Que cela ne nous empêche pas, cependant, de poursuivre encore un peu l’examen de ce que nous appellerons désormais gamme de Helmholtz, afin de rappeler quelques notions élémentaires sur le calcul des intervalles musicaux.
Tous les degrés de cette gamme sont, avec sa tonique ut, dans un rapport de fréquences simple, correspondant à ce qu’on appelle des intervalles « purs14 » : ut1-ut2 forment une octave de rapport 2, ut1-sol une quinte de rapport 3/2, ut1-fa une quarte de rapport 4/3, ut1-mi une tierce majeure de rapport 5/4, ut1-ré un ton de 9/8 la-ut2 une tierce mineure de rapport 6/5, si-ut2 un demi-ton (diatonique) de rapport 16/15.
Les difficultés apparaissent dès lors qu’on calcule les intervalles qui figurent entre les degrés intermédiaires, et notamment les secondes, les quintes et les tierces. Tout d’abord, les secondes ré-mi et sol-la sont de rapport 10/9 et conduisent à la définition d’un ton mineur qui oblige à rebaptiser ton majeur le ton traditionnel ou pythagoricien de 9/8. Cette distinction entre un ton mineur et un ton majeur est absente des principaux systèmes d’intonation qui ont historiquement prévalu dans la musique pour clavier (accord pythagoricien, tempéraments mésotonique ou égal…) et, de plus, les règles du contrepoint et, plus tard, de l’harmonie, ne l’ont jamais prise en compte. Ensuite, avec la quinte ré-la apparaît le rapport de 40/27, intervalle que rejetterait, en simultanéité, la moins délicate des oreilles : en comparaison avec la quinte de 3/2, elle est trop petite d’un micro-intervalle qu’on calcule à 81/80 et qu’on appelle comma syntonique (ci après comma tout court). Enfin, la tierce mineure ré-fa est d’un rapport de 32/27, ce qui en fait une tierce mineure pythagoricienne. On notera que c’est aussi le comma qui fait la différence entre le ton majeur et le ton mineur, ainsi qu’entre les tierces pythagoriciennes et les tierces pures.
Afin de pallier ces intervalles irréguliers, dus à l’irruption d’un inévitable grain de sable nommé comma, Helmholtz introduit dans sa gamme un second ré, d’un comma plus grave que le premier15, et qui permet de restituer dans leurs rapports « naturels » la quinte ré-la et la tierce mineure ré-fa. Avec cette note dédoublée, il devient possible de construire, sur la gamme de Helmholtz, les accords parfaits qui permettent d’en dégager une tonalité. Mais il est alors légitime de se demander si une gamme qui présente un degré optionnel est encore une gamme, et comment elle pourra fonctionner comme repère diatonique, du moment qu’un de ses degrés n’est pas déterminé : par quelle variante du ré passer lorsqu’on monte d’ut à mi ? On se demande aussi comment sortir de l’étroit domaine de la « pureté tonale » absolue, car la moindre « modulation » fera intervenir d’autres gammes de Helmholtz, tout aussi indéterminées. Comment le chanteur s’y retrouvera-t-il ? Et, en admettant même qu’il s’y retrouve, comment imaginer qu’il puisse, sur la base de prémisses si anachroniques, s’approcher un tant soit peu des schémas de pensée qui prévalaient à la Renaissance ? C’est dans cette impasse que nous abandonnerons la « gamme naturelle ».
Le système diatonique pythagoricien, tel que décrit par Boèce et la théorie médiévale, est déjà une forme d’intonation juste. Il est en effet bâti exclusivement sur des proportions simples, faisant intervenir les facteurs 2 et 3 : tous les intervalles qu’il comporte sont « non tempérés » et peuvent être réduits à des combinaisons d’octaves (de rapport 2) et de quintes (de rapport 3/2). Repris par ceux qui accordaient les instruments à clavier, il a été arbitrairement limité, à un cycle de douze quintes, la dernière d’entre elles, le fameux loup, trop petite d’un comma dit pythagoricien, traduisant l’incommensurabilité mathématique des puissances de 2 et de celles de 3 ou, ce qui revient au même, l’impossibilité de faire coïncider un nombre donné de quintes avec un nombre donné d’octaves. En réalité, et si l’on refuse tout compromis, une série de quintes pures se présente, abstraction faite des octaves, non comme un cercle mais comme une spirale doublement infinie. C’est cette spirale qui constitue le « noyau » de tout système d’intonation juste. Sous forme déroulée, elle prend l’aspect suivant16 :
…Ebb-Bbb-Fb-Cb-Gb-Db-Ab-Eb-Bb-F-C-G-D-A-E-B-F#-C#-G#-D#-A#-E#-B#-F##-C##-G##-D##-A##…
La principale limitation de ce système est qu’il ne permet pas de générer des tierces pures, majeures (5/4) ou mineures (6/5), mais seulement des tierces pythagoriciennes de 81/64 et de 32/27. La tierce majeure pythagoricienne est, rappelons-le, plus grande d’un comma (syntonique) que la tierce majeure pure, la tierce mineure pythagoricienne est plus petite d’un comma que son homologue pure. L’astuce, exposée notamment par Barbour17, consiste à ajouter, parallèlement à cette série nucléaire de quintes pures, une seconde série décalée d’un comma vers le grave, qui permet de générer des tierces majeures pures à partir de chacune des notes de la première série. Ce qui donne, sur un tronçon limité :
série "-1" : … D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 …
/ \
série de base : … Bb --- F --- C --- G --- D --- A --- E --- B --- F# …
En partant d’une note quelconque de la série de base (par exemple C) et en montant en oblique vers la droite, on obtient la tierce majeure pure (E-1 se trouve un comma en dessous du E de la série de base). En redescendant, toujours en oblique vers la droite, on retombe sur la quinte de la note de départ (G), ce qui complète l’accord parfait majeur. Plus généralement, après avoir ajouté une série de quintes, on a accès, à partir de chacune des notes de la série de base, à la tierce majeure vers l’aigu et à la tierce mineure vers le grave.
Mais tous les problèmes ne sont pas pour autant résolus. Afin de pouvoir générer, à partir de chacune des notes de la série de base, des tierces majeures vers le grave et des tierces mineures vers l’aigu, il faut maintenant ajouter au système une série de quintes décalée d’un comma vers l’aigu :
série "-1" : … D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 …
/ \
série de base : … Bb --- F --- C --- G --- D --- A --- E --- B --- F# …
\ /
série "+1" : … Db+1 Ab+1 Eb+1 Bb+1 F+1 C+1 G+1 D+1 …
En descendant en oblique vers la droite, et en remontant symétriquement, il est possible d’obtenir n’importe quel accord parfait mineur. La combinaison de ces trois séries de quintes permet donc de générer, à partir de chacune des notes de la série de base, un accord parfait majeur et un accord parfait mineur. Cela peut sembler satisfaisant, mais que se passe-t-il lorsque, à partir d’une note de l’une des séries ajoutées, on désire générer une nouvelle tierce pure ? On doit avoir recours à une série de quintes supplémentaires, décalée d’un comma par rapport à la précédente, et ainsi de suite à l’infini vers le haut comme vers le bas :
…
série "-3" : … A#-3 E#-3 B#-3 F##-3 C##-3 G##-3 …
série "-2" : … F#-2 C#-2 G#-2 D#-2 A#-2 E#-2 B#-2 …
série "-1" : … D-1 A-1 E-1 B-1 F#-1 C#-1 G#-1 D#-1 …
/ \
série de base : … Bb --- F --- C --- G --- D --- A --- E --- B --- F# …
\ /
série "+1" : … Db+1 Ab+1 Eb+1 Bb+1 F+1 C+1 G+1 D+1 …
série "+2" : … Fb+2 Cb+2 Gb+2 Db+2 Ab+2 Eb+2 Bb+2 …
série "+3" : … Abb+3 Ebb+3 Bbb+3 Fb+3 Cb+3 Gb+3 …
…
Voilà donc enfin un « système complet de génération d’accords purs », pour reprendre l’expression d’Asselin18. Ce réseau représente toutes les fréquences qu’il est possible d’atteindre en procédant par combinaisons de quintes et de tierces pures, au départ d’un point unique (par exemple A440). Il est impressionnant parce qu’il est quatre fois illimité : chaque série de quintes est deux fois illimitée, vers la gauche et vers la droite, et il est possible d’ajouter une double infinité de séries de quintes, au-dessus et au-dessous de la série de base. Si l’on se souvient, de plus, qu’il avait été fait, au départ, abstraction des octaves, on peut maintenant, parallèlement au plan de la feuille (ou de l’écran), superposer à ce réseau bidimensionnel déjà fort complexe des copies conformes de lui-même, transposées d’une ou plusieurs octaves, et cela à l’infini vers l’aigu comme vers le grave, pour obtenir toutes les fréquences atteignables en théorie (la théorie ne s’arrête pas avec les limites de la phonation et de l’audition humaines !) en combinant des octaves, des quintes et des tierces pures. On comprend qu’une telle structure ait pu donner le vertige à certains auteurs, comme à D. Devie, qui n’en livre pas moins une description très imagée :
On peut imaginer un immense labyrinthe sous la forme d’une construction faite d’une série d’étages comportant, à chaque niveau, un couloir en forme de spirale qui se déroulerait à l’infini en cercles concentriques vers la périphérie. Tous les 5 mètres, on trouverait un escalier montant à l’étage supérieur ou descendant à l’étage inférieur, représentant les tierces pures. Qu’on se représente le moindre accord parfait à l’intérieur de ce dédale et l’on aura une idée du caractère aberrant du système en question19.
Le vertige provient avant tout de l’incroyable surabondance de fréquences que recrute un tel labyrinthe, et à l’impossibilité de concevoir un clavier qui les prenne toutes en compte : les tentatives en ce sens ont conduit à quelques curiosités de la facture instrumentale qui n’ont jamais dépassé le stade du prototype20.
C’est un vertige d’un autre ordre qui prend le chanteur s’il tente de s’engager dans le labyrinthe de Barbour. Sa voix, extrêmement flexible, n’est en effet pas soumise à la principale faiblesse des claviers : un nombre limité de touches par octave. S’il perd néanmoins pied, c’est avant tout parce qu’il ne sait quel chemin prendre pour passer d’une note à l’autre. En d’autres termes, le labyrinthe de Barbour, qui ne procède que par tierces, quintes et octaves, est totalement dépourvu de repère diatonique : en aucune manière, il n’indique comment procéder par degrés. L’intervalle de seconde, maillon élémentaire de toute mélodie, n’y apparaît jamais de manière directe.
Faute de mieux, Barbour21, qui a bien vu les faiblesses de la gamme de Helmholtz et son inaptitude à fonctionner en elle-même comme repère diatonique, se raccroche à ce qu’on peut appeler le principe de la note commune : il postule que, lorsqu’une note est commune à deux accords consécutifs, elle ne doit pas varier. Le résultat est que certains enchaînements d’accords vont entraîner une instabilité du diapason22 qui, au cas où le phénomène se répète, peut se transformer en une véritable dérive. Il prend l’exemple suivant :

Figure 1.2 : Le début du God save the King.
Si l’on admet que le A du quatrième accord doit être le même que celui du troisième, l’accord de G majeur qui clôt cet extrait se retrouve un comma plus grave que l’accord initial. En répétant en boucle les deux premières mesures du célèbre chant, on obtient cette curieuse descente aux enfers (Exemple 1.1)23. Il suffit, nous semble-t-il, de l’entendre une seule fois pour se rendre compte de son caractère invraisemblable : aucun ensemble vocal, fût-il médiocre ou au contraire excellent, ne saurait reproduire un tel naufrage, et encore moins s’en faire un modèle.
Appliqué systématiquement, le principe de la note commune, ou tout principe analogue, provoquerait, dans d’innombrables pièces, des dérives du diapason identiques à celle du God save the King. Barbour se sert cette observation pour construire une réfutation fondamentale de l’intonation juste. En toute logique, ce n’est que le principe de la note commune qu’elle aurait pu rendre caduc. Curieusement, il n’en a rien été : ce même principe a été récupéré depuis, sous une forme plus générale, par les partisans mêmes de l’intonation juste. C’est ainsi que, parmi les interprètes spécialisés dans la polyphonie vocale, il n’est pas rare d’entendre l’opinion, à notre avis farfelue, selon laquelle, si l’on chante « vraiment » juste, alors le diapason « doit » fluctuer. L’idée est à ce point reçue qu’on la trouve, reprise telle quelle, dans des écrits théoriques récents24. Si l’on relève, avec un rien d’ironie, qu’il est certainement plus gratifiant pour un groupe de chanteurs de se dire qu’ils détonnent parce qu’ils chantent « trop » juste que d’admettre qu’ils chantent faux ou « pas tout à fait » juste, on comprend d’autant mieux l’apparition d’un tel mythe.
Ce dont on ne s’est guère avisé, cependant, c’est que le principe de la note commune, et donc la dérive du diapason, ne sont en rien inéluctables. Pourquoi, en effet, le ténor qui chante God save the King devrait-il forcément calquer son A du quatrième accord sur le A chanté par le soprano au troisième accord, forçant par là même les autres voix à s’adapter et le diapason à baisser ? Ne pourrait-on pas attendre que l’alto et la basse tombent plutôt d’accord sur le D qui est déjà présent dans l’accord initial (en langage tonal, la dominante) ? Le soprano n’aurait ensuite guère de peine à les rejoindre en chantant une tierce pythagoricienne descendante A-F#. Enfin, ces trois voix forceraient le ténor à ajuster son A un comma au-dessus de celui qu’il vient d’entendre au soprano. Cette seconde solution est-elle, sur le papier, plus invraisemblable que la première, elle qui a l’avantage de maintenir aussi bien le diapason que la pureté verticale et n’est, même répétée en boucle, nullement choquante pour l’oreille (Exemple 1.2) ? Au nom de quoi la première solution, celle qui « sonne faux » serait-elle représentative de l’intonation juste, alors que la seconde, celle qui « sonne juste », serait exclue de cette définition ?
Comment aller plus loin, face à toutes ces questions ? C’est Zarlino et la théorie du xvie siècle qu’il va maintenant falloir questionner.
Répétons-le : c’est en vain qu’on cherche chez Zarlino la clef de la pratique de l’intonation juste. En fait, ses préoccupations sont avant tout théoriques25. Lorsqu’il calcule les intervalles selon les préceptes de Ptolémée, c’est un système purement spéculatif et abstrait qu’il produit. Et lorsqu’il en fait le principe de l’intonation des chanteurs, il ne dit pas avec précision comment ils doivent ou peuvent l’utiliser. On voudrait bien que, à sa suite, les traités pratiques se soient mis à aborder des problèmes d’intonation. Malheureusement, il subsiste, à la Renaissance, un important fossé entre l’approche spéculative des traités de haut vol comme ceux de Zarlino et l’approche pratique des traités élémentaires qui commencent alors à fleurir mais, étant destinés à des débutants, s’en tiennent le plus souvent aux rudiments.
Dans ce fossé, qui sépare écrits théoriques et pratiques, s’est trouvée engloutie une bonne partie de ce qui constituait le « métier » des meilleurs interprètes de la Renaissance : c’est là qu’il faut aller chercher la réponse à nos questions. L’expédition, on le comprend, est périlleuse et son résultat hasardeux. Nous pensons néanmoins qu’elle en vaut la peine : on n’a pas, à ce jour, fait dire à Zarlino tout ce qu’il pouvait dire. Il nous semble en particulier que l’imposition de notions modernes comme celles de gamme et de tonalité, ou alors le recours à l’image du clavier, ont eu un effet de brouillage considérable sur la compréhension de sa théorie. Nous préférerons oublier ces notions et nous efforcer de suivre les étapes du raisonnement de Zarlino en épousant ses propres concepts, quitte à en poursuivre la logique un peu plus loin qu’il ne l’a fait lui-même, mais comme il est vraisemblable qu’aient pu le faire ceux de ses lecteurs du xvie siècle qui étaient à la recherche de clefs pour pratiquer l’intonation juste. C’est de cette manière que nous tenterons de parvenir à un modèle utilisable, conjectural bien sûr mais, nous l’espérons, plausible.
Tirant ses origines mythologiques de la lyre de Mercure et d’Orphée26, le tétracorde est un des piliers de la théorie grecque antique. Comme son nom l’indique, il comporte quatre cordes27 dont les deux extrêmes forment un intervalle de quarte28, de rapport 4/3. La disposition des deux cordes centrales est fonction du genre, diatonique chromatique ou enharmonique, ainsi que de l’espèce, c’est-à-dire en gros du principe d’intonation choisi. Très schématiquement, et de bas en haut, un tétracorde diatonique se compose d’un demi-ton surmonté de deux tons, un tétracorde chromatique de deux demi-tons (en principes inégaux) surmontés d’un grand intervalle complétant la quarte, un tétracorde enharmonique de deux diesis qui forment, ajoutés l’un à l’autre, un demi-ton qu’ils divisent de manière pratiquement égale, surmontés d’une tierce majeure.
Conformément à l’esprit de la Renaissance, Zarlino ne se limite pas à Boèce et aux tétracordes pythagoriciens : il s’efforce de remonter à d’autres sources antiques, et notamment à Ptolémée29, ce qui lui permet de comparer, pour chacun des trois genres, plusieurs espèces, caractérisées par des proportions spécifiques. C’est avant tout le genre diatonique qui va nous intéresser, et la comparaison, appliquée au tétracorde, de deux espèces, dont Zarlino a trouvé la description chez Ptolémée, et qu’il appelle respectivement diatonico diatono (ou plus brièvement diatono) et diatonico sintono (ou sintono tout court).
Le diatono n’est autre que le diatonique pythagoricien30 : il conduit à un tétracorde dans lequel un demi-ton de 256/243 est surmonté de deux tons de 9/8 chacun.

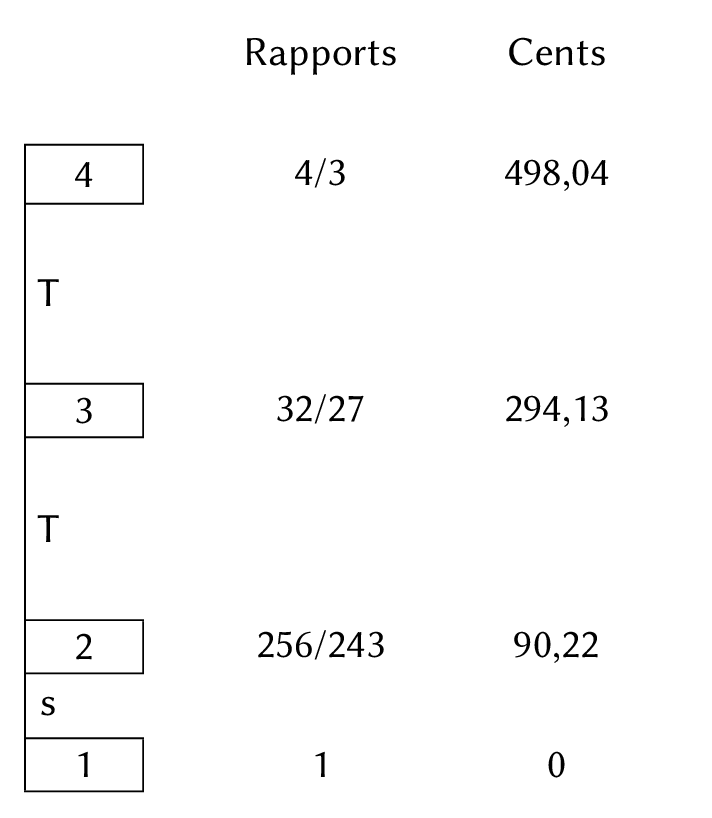
Figure 2.1 : Le tétracorde diatonique de l’espèce diatono.
Ces rapports se retrouvent bien entre les nombres indiqués par Zarlino : de bas en haut, 8192, 7776, 6912, 6144. Comme il raisonne en termes de longueur de corde, ils sont bien entendu inverses de ceux qu’on obtient en raisonnant en termes de fréquence, et qu’on trouve sur notre schéma : les degrés du tétracorde y sont numérotés de bas en haut, accompagnés du rapport de fréquences qu’ils entretiennent avec le degré inférieur, puis par la valeur de cet intervalle en cents31. Les caractéristiques principales de ce tétracorde sont donc le « petit » demi-ton (s) de 90 cents (par définition, le demi-ton tempéré en compte 100) et les deux « grands » tons égaux de 204 cents (T).
Pour le tétracorde diatonique de l’espèce sintono, qui est « celui que les modernes utilisent dans leurs harmonies32 », Zarlino donne, de bas en haut, les nombres 48, 45, 40 et 36, entre lesquels on trouve un « grand » demi-ton de 16/15 (S), soit 112 cents, un ton majeur (T) de 9/8 et un ton mineur (t) de 10/9, soit 182 cents.


Figure 2.2 : Le tétracorde diatonique de l’espèce sintono.
Le sintono se distingue donc par le fait que les deux degrés intermédiaires du tétracorde sont placés un comma plus haut que ceux du diatono, avec pour résultat que les deux tierces, mineure et majeure, qui figurent entre les degrés 1-3 et 2-4 respectivement sont des tierces pures. Les quatre degrés du tétracorde de l’espèce diatono étant pris, par définition, dans la même série de quintes pures, les deux degrés intermédiaires de celui de l’espèce sintono appartiennent donc à une série d’un comma plus élevée. A ce stade déjà, on constate que le sintono permet, en procédant par degrés, de puiser dans deux séries de quintes distinctes, avec pour résultat la production de tierces pures. Un seul tétracorde ne mène pas bien loin, mais il n’en constitue pas moins l’embryon du repère diatonique dont nous avons besoin.
Composé d’une seule très longue corde divisée par un chevalet mobile, le monocorde a de tout temps été employé pour les spéculations sur les intervalles musicaux. C’est lui qui va permettre de calculer les proportions de ce que Zarlino appelle le sistema massimo33 : le modèle antique à seize cordes, organisé en cinq tétracordes immuablement disposés les uns par rapport aux autres (Figure 2.3 et Figure 2.4).
A la base, une corde isolée (le proslambanomenos), surmontée, un ton au-dessus, par deux tétracordes superposés, ou plutôt joints, car la corde supérieure du premier, celui des cordes graves (hypaton), se confond avec la corde inférieure du second, celui des moyennes (meson). La corde supérieure du tétracorde des moyennes est la corde centrale, ou mese. Suivent, un ton au-dessus, le tétracorde des disjointes (diezeugmenon), ainsi nommé parce que, justement, un ton le sépare du tétracorde des moyennes et, finalement, le tétracorde des aiguës (hyperboleon), lui-même joint au tétracorde des disjointes.
On ajoute encore, à partir de la mese, le tétracorde des conjointes (synemennon), dont le deuxième degré apporte un nouveau demi-ton entre la mese et le tétracorde des disjointes, ce qui permet d’éviter le triton apparaissant entre le deuxième degré du tétracorde des moyennes (parhypate meson) et le premier degré de celui des disjointes (paramese). Il est important de noter ici que, dans le diatono, ce tétracorde ne fournit en fait qu’une seule corde supplémentaire, celle du demi-ton : ses premier, troisième et quatrième degrés se confondent avec des cordes déjà présentes. Il ne pouvait toutefois être question de n’ajouter qu’une seule corde, comme on ajouterait, par exemple, une touche noire entre deux touches blanches d’un clavier. Au contraire, ce demi-ton devait trouver sa place dans un tétracorde, lui-même ancré dans le système complet. Nous avons là une première illustration de la manière dont une structure modulaire, ici un système de tétracordes, peut servir de repère diatonique.
Dans le sistema massimo, les bornes de chaque tétracorde sont immuables. Seules peuvent changer, conformément à la définition du tétracorde, leurs cordes intermédiaires. Ainsi, si l’on se limite au genre diatonique, c’est l’espèce qui déterminera la position précise des cordes intermédiaires de chaque tétracorde. Zarlino peut donc se livrer, pour chaque espèce décrite, à un calcul précis des proportions du sistema correspondant.
Il commence par le faire pour le diatono34 (Figure 2.3), c’est-à-dire pour le pythagoricien traditionnel. Afin de pouvoir attribuer des nombres entiers à toutes les cordes, il donne la valeur 921635 à la note la plus grave (proslambanomenos). La progression par degrés s’opère par demi-tons de 256/243 (s) et par tons de 9/8 (T) exclusivement. Zarlino ne peut s’empêcher de critiquer ce système, pourtant communément admis depuis plusieurs siècles : les tierces majeures et mineures de 81/64 et 32/27 le gênent profondément. Pour lui en effet, une consonance ne peut correspondre qu’à une proportion du genre multiple (double, triple, quadruple etc.) ou du genre superparticulaire (dont le numérateur n’excède le dénominateur que d’une unité : 3/2, 4/3, 5/4, 6/5). Comme elles ne répondent pas à ces conditions, les tierces pythagoriciennes sont forcément dissonantes, ce qui entre en contradiction avec la pratique musicale courante, dans laquelle les tierces fonctionnent bel et bien comme des consonances36.
C’est de cette manière que Zarlino motive sa préférence pour un système fondé sur le sintono, caractérisé, justement, par le fait qu’il ne contient que des proportions superparticulaires : 16/15 pour le demi-ton (S), 10/9 et 9/8 pour les tons mineur (t) et majeur (T), 6/5 pour la tierce mineure, 5/4 pour la tierce majeure et 4/3 pour la quarte. Partant d’un proslambanomenos à 864, il peut attribuer un nombre entier à toutes les cordes37. Globalement, ce système est très proche de celui bâti sur le diatono. Une différence de taille, cependant : le quatrième degré du tétracorde des conjointes (nete synemennon) qui, dans le diatono classique, se confondait avec le troisième degré du tétracorde des disjointes (paranete diezeugmenon), est maintenant plus grave d’un comma, comme l’illustrent les nombres de 324 et de 320 que Zarlino calcule pour eux (Figure 2.5). Sur notre schéma (Figure 2.6), on voit que c’est la rencontre d’un ton majeur et d’un ton mineur qui est responsable de cette distorsion.
Nous nous trouvons en présence d’un phénomène analogue à celui de la « note dédoublée » de la gamme de Helmholtz. Seulement, alors que ce dédoublement d’un degré est un phénomène déstructurant dans le cas d’une gamme majeure au sens de la théorie moderne, il n’en est absolument rien ici : les modules du système, c’est-à-dire les tétracordes, ne se trouvent nullement affectés dans les rapports que, par leurs bornes et de degré à degré, ils entretiennent les uns avec les autres. Et il y a plus : le système, qui semblait redondant dans sa version pythagoricienne, puisque certaines cordes avaient des noms différents tout en étant confondues du point de vue de leur longueur (et donc de leur fréquence), dispose en fait déjà d’un nom distinct pour chacune de ces cordes décalées d’un comma (paranete diezeugmenon et nete synemennon) : chacune d’entre elles entretient des relations parfaitement bien définies avec les autres cordes de son tétracorde respectif et le système dans son ensemble peut continuer à fonctionner sans heurts.
Dans sa version syntonique (c’est-à-dire fondée sur l’espèce sintono de Ptolémée-Zarlino), le grand système à seize cordes des Grecs s’adapterait parfaitement aux idéaux de l’intonation juste s’il pouvait être, pour la musique de la Renaissance, d’une quelconque utilité pratique. Ce n’est évidemment pas le cas : de système pratique dans l’Antiquité, il est devenu, au Moyen Âge et à la Renaissance, référence théorique première et support de toute spéculation sur les intervalles, mais il a perdu tout lien avec la pratique musicale. En fait, il a été remplacé par un système plus étendu de 22 cordes qui, comme lui, présente une structure modulaire. Le module n’est plus ici le tétracorde mais l’hexacorde, selon la tradition attribuée à Gui d’Arezzo.
Comme l’explique Zarlino38, l’hexacorde contient en son milieu le demi-ton qui se trouvait à la base du tétracorde, ce qui signifie qu’il consiste en une extension du tétracorde vers le bas, par adjonction de deux degrés d’un ton.

Figure 2.7 : L’hexacorde de l’espèce diatono.
De bas en haut, les degrés de l’hexacorde se voient attribuer les syllabes rituelles ut, ré, mi, fa, sol et la, qui remontent elles aussi à Gui d’Arezzo (et, bien sûr, à l’hymne Ut queant laxis) et qui viennent remplacer avantageusement les noms grecs.
Zarlino ne se prive pas de calculer les rapports de l’hexacorde pythagoricien (Figure 2.8). Ses six degrés se voient attribuer, par exemple, les nombres 10368, 9216, 8192, 7776, 6912 et 6144, entre lesquels on retrouve quatre tons de 9/8 encadrant un demi-ton de 256/243. Le système complet de 22 cordes, souvent appelé main guidonienne en révérence à Gui d’Arezzo39, comporte sept hexacordes. Tout comme l’hexacorde est une extension du tétracorde, la main guidonienne est une extension du système des Grecs, et le contient donc : sur notre schéma (Figure 2.9), les cordes et les tétracordes du système des Grecs apparaissent en gris.
On note, tout à gauche, les clefs (en fait, les lettres de A à G), qui ancrent le jeu d’hexacordes dans une échelle absolue40. Ces clefs préfigurent l’usage qui a prévalu aujourd’hui dans les pays anglo-saxons pour désigner les notes. Elles apparaissent en majuscules pour l’octave inférieure (de A à G), en minuscules pour l’octave moyenne (de a à g) et en minuscules doubles pour l’octave aiguë (de aa à ee, la main étant limitée, vers le haut comme vers le bas).
Les cinq tétracordes du système des Grecs se retrouvent intacts dans la main guidonienne, où ils entretiennent les mêmes rapports que dans le système d’origine. Ils ont simplement été transformés en hexacordes, et donc agrandis de deux degrés vers le bas. L’extension du tétracorde des graves a entraîné l’ajout d’une corde supplémentaire, un ton au-dessous du proslambanomenos (A) : le gamma qui a donné son nom à notre moderne gamme.
Le système des Grecs a, de plus, été étendu vers le haut, par adjonction de deux hexacordes, partant de f et g. Les deux hexacordes basés sur un C sont appelés naturels, les trois basés sur un G sont appelés durs et les deux basés sur un F sont appelés mols. Aux deux octaves supérieures, la clef B existe sous deux variantes, l’une, dure ou carrée (bécarre) fonctionnant comme mi d’un hexacorde dur et correspondant au B naturel, l’autre, molle (bémol), fonctionnant comme fa d’un hexacorde mol et correspondant au Bb41. Bien qu’elle comporte des cordes correspondant à des notes « altérées » (bémols), la main reste une structure strictement diatonique.
Du fait de l’extension de chaque tétracorde en un hexacorde, ceux-ci se chevauchent bien plus que ceux-là et les cordes confondues, qui étaient occasionnelles dans le système des Grecs, deviennent, on le voit, très nombreuses dans la main guidonienne : six clefs sont communes à trois hexacordes distincts, huit clefs à deux hexacordes. Seules huit clefs sont spécifiques d’un seul hexacorde. La redondance est donc ici érigée en principe.
Contrairement à l’usage qui a prévalu aujourd’hui dans les pays latins, les syllabes ut, ré, mi, fa, sol et la, appelées voix, ne correspondent pas à des hauteurs absolues dans l’échelle, mais seulement aux six degrés d’un hexacorde, leur hauteur absolue dépendant de la situation dudit hexacorde dans la main guidonienne. Lorsqu’on voulait, à la Renaissance, désigner un degré de la main de manière complète, il était d’usage de faire suivre la clef correspondante de la voix ou des voix qu’elle pouvait recevoir, en commençant par l’hexacorde le plus grave. Ainsi, ce qui est aujourd’hui un G dans certains pays et un sol dans d’autres se déclinait-il G sol-ré-ut42.
Voilà donc le système qui a, durant près de six siècles, servi de base à l’enseignement musical. Inculquée à la baguette à des générations d’enfants de chœur, et donc profondément enracinée dans les représentations mentales et les automatismes de tout chanteur de cette longue période, la main guidonienne a durablement constitué le repère diatonique universel grâce auquel on s’orientait dans l’échelle musicale, en servant de support à la solmisation43.
En pratique, le chanteur qui déchiffre une mélodie en solmisant utilise tout d’abord les voix de l’hexacorde dans lequel cette mélodie évolue. Si elle dépasse les limites d’un seul hexacorde (ce qui est le cas le plus fréquent), il effectue une muance (en latin mutatio), c’est-à-dire qu’il change d’hexacorde : il substitue à une voix de l’hexacorde de départ, la voix de l’hexacorde d’arrivée qui se trouve à la même hauteur. Il exploite donc la redondance du système et se déplace en quelque sorte le long des lignes horizontales de notre schéma (Figure 2.9).
Un avantage de l’hexacorde sur la gamme moderne est qu’il ne contient pas de triton (la gamme majeure en recèle un entre son quatrième et son septième degré), ni d’autre consonance parfaite augmentée ou diminuée. Ainsi, tant qu’il évolue au sein d’un hexacorde donné, le chanteur n’a aucunement besoin de se soucier d’éviter, par exemple, quarte augmentée ou quinte diminuée. Ce n’est que lorsqu’il fait une muance qu’il doit être attentif au problème. Dans le cadre d’une pratique musicale soumise au dogme de l’évitement de tels intervalles, cette particularité du système a une grande importance.
Un autre atout important de la main guidonienne et de la solmisation est que tous les demi-tons y ont le même statut : ils s’y chantent mi-fa. C’est de part et d’autre de cet intervalle central que s’organisent les tons ut-ré, ré-mi, fa-sol et sol-la de chaque hexacorde. Les huit modes ecclésiastiques ayant tous, sous leur forme canonique, leur finale sur D, E, F, et G, qui sont le ré, le mi, le fa et le sol de l’hexacorde naturel, il est possible, en partant d’une formule mélodique écrite dans un mode quelconque, de la transposer d’une quarte, d’une quinte ou d’une octave sans modifier aucunement le nom des voix sur lesquelles elle sera chantée. Ainsi, alors que, transposé d’une quarte, D-E-F donne G-A-Bb dans le système anglo-saxon, alors que ré-mi-fa donne sol-la-si bémol dans le système latin, ré-mi-fa reste ré-mi-fa en solmisation. De plus, quel que soit l’hexacorde dans lequel on la chante, une formule du premier mode aura sa finale sur ré, une formule du cinquième sur fa, etc. On peut voir dans cette caractéristique la principale raison d’être du système : une adaptation du grand système des Grecs dans le but de le rendre compatible avec les modes ecclésiastiques.
Les sept hexacordes de la main guidonienne constituent ce qu’il est convenu d’appeler la musica recta (musique vraie). Il est possible, par exemple pour éviter des tritons, d’ajouter un ou plusieurs autres hexacordes au système, soit en direction « molle », c’est-à-dire en montant par quartes ou en descendant par quintes sur la droite de notre schéma, soit en direction « dure », c’est-à-dire en montant par quintes ou en descendant par quartes sur la gauche de notre schéma. Ces hexacordes virtuels ou feints, non compris dans la main guidonienne, appartiennent à la musica ficta (musique feinte). Chaque hexacorde ajouté dans la direction « molle » ajoute un fa au système, qui correspond, en termes modernes, à un bémol. Chaque hexacorde ajouté dans la direction « dure » ajoute un mi au système, qui correspond, en termes modernes, à un dièse.
Résumons : nous avons suivi la transformation du tétracorde pythagoricien en un hexacorde, ainsi que, parallèlement, celle du sistema massimo de l’espèce diatono en ce qu’on peut appeler une main pythagoricienne, qui constitue le repère diatonique universellement admis au Moyen Âge et à la Renaissance. Parallèlement, nous avons appris que, comme principe d’intonation, l’espèce diatono n’est pas satisfaisante pour une oreille renaissante : elle pèche par ses tierces, qui sont loin d’être pures. Nous savons aussi que c’est l’espèce sintono qui a les faveurs de Zarlino et nous disposons par ailleurs du tétracorde et du sistema massimo construits selon ce principe d’intonation. Nous sommes donc à même de synthétiser le tout en une main syntonique, composée d’hexacordes inspirés par le sintono de Ptolémée.
Il s’agit, en toute logique, de la dernière étape du cheminement qui devrait conduire à un repère diatonique qui soit conforme aux idéaux de Zarlino. Si, pour des raisons qu’il est difficile d’élucider, il n’a pas lui-même franchi cette étape, il a néanmoins consciencieusement jalonné le chemin qui y mène. Quiconque avait, à la Renaissance, un intérêt pratique pour l’intonation juste ne pouvait qu’être amené, tout comme nous, à faire ce dernier pas.
Transformer un tétracorde de l’espèce sintono en un hexacorde syntonique consiste bien sûr à l’étendre vers le bas de deux degrés d’un ton. Comme il existe, dans cette espèce, un ton majeur et un ton mineur, on peut hésiter sur la combinaison à adopter. Toutefois, on voit immédiatement que, pour que la sixte ut-la soit pure, il faut ajouter à la quarte mi-la (le tétracorde de départ) une tierce majeure pure, et donc un ton majeur et un ton mineur. D’autre part, pour que toutes les tierces de l’hexacorde (ut-mi, ré-fa, mi-sol et fa-la) restent pures, conformément à la logique du sintono, il faut, c’est la seule solution, placer le ton mineur (t) entre ut et ré, le ton majeur (T) entre ré et mi. On obtient donc une structure symétrique dans laquelle les deux tons extrêmes sont mineurs, les deux tons intermédiaires sont majeurs, le tout encadrant le demi-ton central (S).
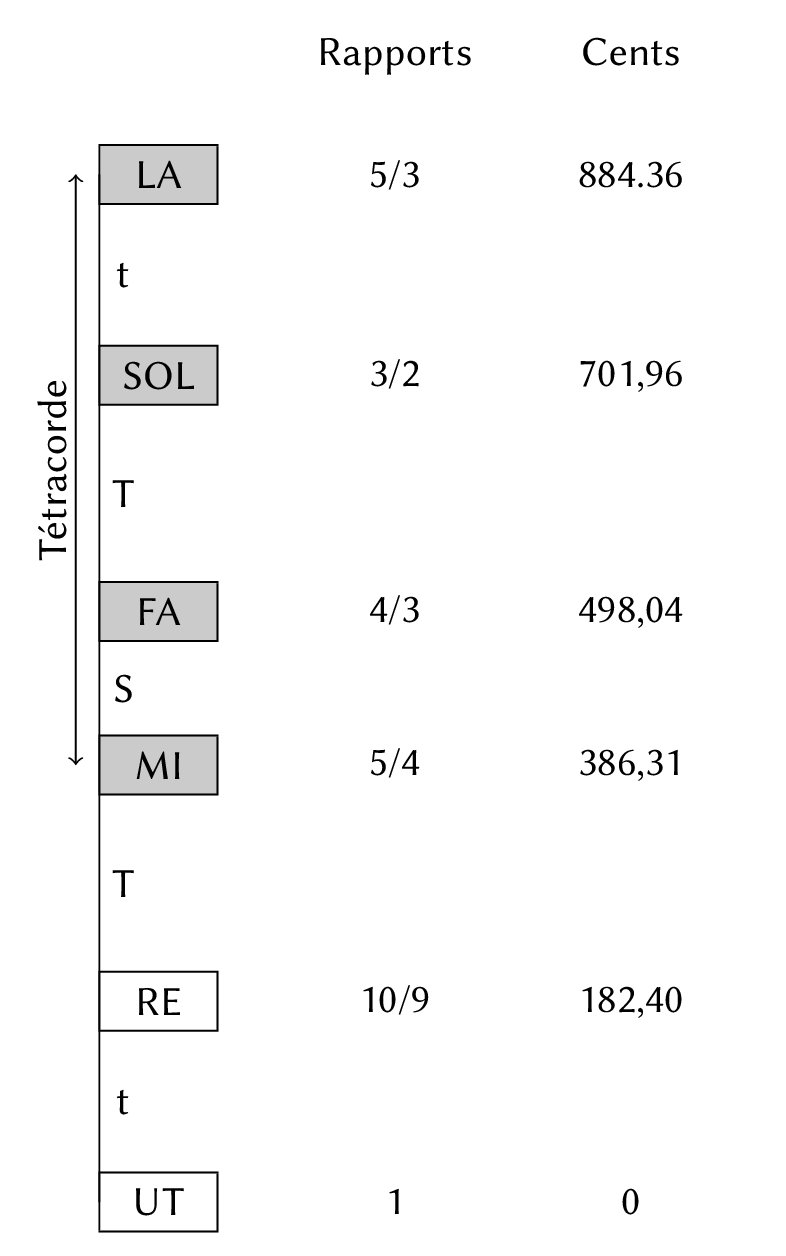
Figure 2.10 : Organisation possible d’un hexacorde syntonique.
Cet hexacorde n’est pas absolument parfait : sa quarte ré-sol est trop grande d’un comma. De quelque manière qu’on tourne le problème, il n’est pas possible de faire mieux.
Il est probable que Zarlino44 aurait choisi de placer le ton majeur entre ut et ré, et le ton mineur entre ré et mi, et qu’il aurait donc préféré la séquence T-t-S-T-t à celle que nous avons retenue (t-T-S-T-t), ce avant tout pour des raisons ayant trait à l’esthétique des nombres. Il s’agit bien sûr d’une option possible mais ce n’est pas celle que nous retenons. Comme nous le verrons plus loin, l’enjeu de ce choix, s’il est négligeable du point de vue théorique, a une certaine importance pratique.
Il reste maintenant à bâtir une main syntonique en juxtaposant, comme il se doit, sept hexacordes (Figure 2.11). On y retrouve, cela n’est pas une surprise, la distorsion de comma qui figurait dans le sistema massimo de l’espèce sintono, entre le tétracorde des conjointes et celui des disjointes : dans la main, elle se trouve en regard de la clef d, entre la voix sol d’un hexacorde dur et la voix ré d’un hexacorde naturel, lui-même confondu avec la voix la d’un hexacorde mol. Mais ce n’est pas tout : l’extension des tétracordes en hexacordes a provoqué d’autres rencontres entre tons mineurs et tons majeurs, et donc d’autres distorsions de comma : quatre, en fait, dans la totalité de la main. Toutes se situent, de gauche à droite (c’est-à-dire du dur vers le mol), entre un sol et un ré.
Une main syntonique de ce type constitue l’aboutissement logique de la chaîne théorique de Zarlino, à laquelle elle ne fait qu’ajouter un dernier maillon. A-t-elle réellement et explicitement, du temps ou à la suite de Zarlino, été formalisée ? A-t-elle pu, de manière implicite seulement, influer sur les habitudes d’intonation de l’époque ? Est-elle au contraire, au même titre que la « gamme naturelle » de Helmholtz, une pure vue de l’esprit ? Nous ne le saurons probablement jamais. Quoi qu’il en soit, il vaut certainement la peine de s’y intéresser car, indépendamment de toute considération historique, elle est en elle-même riche d’enseignements sur le fonctionnement des échelles diatoniques.
Limitée à la musica recta, la main syntonique, peut être étendue par les hexacordes de la musica ficta pour donner un système virtuellement illimité45. On obtient alors la structure « cristalline » dont un fragment constitue notre schéma (Figure 3.1). En réalité, ce cristal syntonique ne fait que répéter à l’infini ce qui est déjà manifeste dans la main : chaque nouvel hexacorde apporte deux cordes nouvelles au système, l’une correspondant à une distorsion de demi-ton, l’autre à une distorsion de comma.
En direction molle (c’est-à-dire vers la droite), tout nouvel hexacorde apporte un fa supplémentaire qu’il n’est pas possible de relier à l’hexacorde de départ et qui correspond, comme dans la main pythagoricienne, à un bémol supplémentaire. Simultanément, il apporte aussi un ré, qui se situe un comma plus bas que le sol de l’hexacorde de départ, ce qui est figuré par un trait oblique sur notre schéma. Cette distorsion de comma permet de rendre pure la tierce mineure qui apparaît entre ce nouveau fa et ce nouveau ré.
En direction dure (c’est-à-dire vers la gauche), tout nouvel hexacorde apporte un mi supplémentaire qu’il n’est pas possible de relier à l’hexacorde de départ et qui correspond, comme dans la main pythagoricienne, à un dièse supplémentaire. Simultanément, il apporte aussi un sol, qui se situe un comma plus haut que le ré de l’hexacorde de départ. Cette distorsion de comma permet de rendre pure la tierce mineure qui apparaît entre ce nouveau mi et ce nouveau sol.
Il faut bien voir que c’est l’apparition d’un nouveau demi-ton qui provoque la distorsion de comma : pour pouvoir entrer dans la composition de tierces mineures, tout demi-ton diatonique doit être entouré de tons majeurs. Notre schéma cristallin n’est pas en lui-même responsable de ce lien de cause à effet, qui fait partie des contraintes fondamentales du sintono, il n’est qu’une manière de le représenter
Le système pythagoricien ne faisant appel qu’à une seule série de quintes pures, un hexacorde pythagoricien peut être représenté, abstraction faite des octaves, par six notes consécutives de la série de base du labyrinthe de Barbour, dans l’ordre fa-ut-sol-ré-la-mi, comme le montre le « viseur » gris que nous avons placé, sur notre schéma, en regard des notes qui constituent les clefs de l’hexacorde naturel.

Figure 3.2 : L’hexacorde pythagoricien dans le labyrinthe de Barbour.
Le passage du naturel au dur consiste à déplacer ledit viseur d’un cran vers la droite et se traduit par la perte d’un fa (F) et le gain d’un mi (B). Le passage du naturel au mol consiste à déplacer le viseur d’un cran vers la gauche. Il se traduit par la perte d’un mi (E) et le gain d’un fa (Bb). Les autres notes incluses dans le viseur (C, G, D, A) sont celles qui sont communes aux trois hexacordes. Elles changent simplement de voix. La main pythagoricienne se résume donc à huit notes consécutives sur la série de base du labyrinthe de Barbour. Mais il est également possible de s’aventurer dans la musica ficta : il suffit pour cela de déplacer le viseur par crans successifs, vers la droite comme vers la gauche. Lors d’un mouvement vers la droite, une note donnée, par exemple B, va entrer dans le champ du viseur comme un mi, puis elle passera successivement par les voix la, ré, sol, ut, fa, avant d’en sortir, ce au fur et à mesure que l’hexacorde visé progressera en direction dure. Des observations inverses peuvent être faites pour le mouvement vers la gauche.
Comme le labyrinthe de Barbour est exhaustif, la main syntonique doit bien y être comprise aussi. Essayons de comprendre comment : les tierces de l’hexacorde syntonique étant toutes pures, leurs extrémités appartiennent nécessairement à deux séries de quintes voisines, ce qui va transformer notre viseur en un parallélogramme, à cheval sur deux séries de quintes. Si nous ancrons le a la-mi-ré de la main sur le A de la série de base du labyrinthe, l’hexacorde naturel correspondra, abstraction faite des octaves, à la position de ce nouveau viseur sur le schéma ci-dessous :

Figure 3.3 : L’hexacorde syntonique dans le labyrinthe de Barbour.
En haut, sur la série de base, ré, la et mi, correspondent respectivement à D, A et E ; en bas, sur la série « +1 », fa, ut et sol correspondent à F, C et G. Pour obtenir un hexacorde dur, il faudra déplacer le parallélogramme d’un cran vers la droite, avec pour résultat un nouveau mi (B) et un nouveau sol (D+1). Du même coup, on perdra un fa (F+1) et un ré (D). Pour obtenir un hexacorde mol, il faudra au contraire déplacer le parallélogramme d’un cran vers la gauche, avec pour résultat un nouveau fa (Bb) et un nouveau ré (G). On perdra du même coup un mi (E) et un sol (G+1). Les autres notes, à savoir A et C+1 sont communes aux trois hexacordes et ne font que changer de voix.
La main syntonique représente, on le voit, un minuscule sous-ensemble du terrifiant labyrinthe de Barbour. En fait, un clavier à dix touches par octave lui suffirait. Un système si restreint peut-il servir à la pratique musicale ? Oui, répondrons nous, mais à condition de ne pas sortir de la musica recta, condition à laquelle fort peu de pièces musicales satisfont. Il est donc nécessaire de l’étendre à la musica ficta. A nouveau, il faut, pour ce faire, déplacer le viseur par crans vers la droite ou vers la gauche pour obtenir de nouveaux hexacordes en direction molle ou dure. Suivons le mouvement par crans successifs du viseur vers la droite : une note donnée, (par exemple le B de la série de base), fait son entrée comme mi dans le champ du viseur. Elle passe ensuite par les voix la et ré avant de sortir du champ. Mais le même mouvement qui voit sa variante de la série de base quitter le champ du viseur voit aussi sa variante de la série « +1 » entrer dans ce même champ sous la forme d’un sol. Elle passe ensuite par ut et fa avant de quitter définitivement le champ. On retrouve ce parcours en lisant de droite à gauche les lignes horizontales du cristal syntonique, où la distorsion de comma entre ré et sol est figurée par un trait oblique. Autrement dit, les voix apparaissant à droite (et en dessus) de ce trait oblique, soit fa, ut et sol, appartiennent toujours à la série « +1 » alors que les trois autres, ré, la et mi, appartiennent toujours à la série de base.
On voit maintenant que le cristal syntonique, aussi loin qu’on l’étende, ne fait appel qu’à deux séries du labyrinthe de Barbour. Il en représente une version développée, organisée de manière à faire apparaître les rapports diatoniques existant entre les notes de ces deux séries. Contrairement à ce qui caractérise les claviers, le nombre total de fréquences qu’il recrute par octave n’est pas fixé, mais dépend de l’amplitude de l’excursion faite dans le domaine de la musica ficta : chaque nouvel hexacorde feint apporte au système deux fréquences nouvelles, l’une correspondant à ce qu’on appelle aujourd’hui une altération (dièse ou bémol), l’autre à une distorsion de comma. Le cristal permet de parcourir sans limitation les deux séries de quintes qu’il réunit, et ce degré par degré, en réglant la succession des tons majeurs, des tons mineurs et des demi-tons de manière à produire le plus grand nombre possible de consonances pures. Avons-nous trouvé le repère diatonique que nous cherchions ? Il faudra encore le mettre à l’épreuve de la musique pratique…
La méthode ancestrale de solmisation, fondée sur la main pythagoricienne, laisse aux chanteurs une liberté considérable dans le choix des voix, et donc des hexacordes. Ils peuvent notamment évoluer à leur guise entre deux hexacordes adjacents en utilisant leurs cordes redondantes, correspondant aux lignes horizontales de la main guidonienne, comme supports des muances. Une contrainte majeure, cependant : ils sont tenus d’éviter, pour tous les intervalles constituant historiquement des « consonances parfaites » à savoir les unissons, les quartes, les quintes et les octaves, la rencontre des voix mi et fa, et ce aussi bien horizontalement (mélodiquement) que verticalement (d’une voix à l’autre, en simultanéité).
La raison d’être d’une telle contrainte est claire : les tritons, les quintes diminuées, les octaves et unissons imparfaits, tous en principe interdits par les règles du contrepoint, apparaissent exclusivement entre les voix mi et fa de deux hexacordes, adjacents ou plus distants. Si l’on élargit la main aux hexacordes de la musica ficta, tout cela reste valable : tous les hexacordes entretiennent des rapports rigoureusement semblables avec leurs voisins. On comprend la formidable portée pédagogique de cette particularité de la solmisation : une règle unique suffit à synthétiser l’ensemble des intervalles proscrits. A ceux qui ne sont pas accessibles aux longues spéculations mathématiques (les enfants, par exemple), il suffit de l’enseigner pour les protéger d’un nombre considérable d’erreurs de lecture à vue.
Du point de vue de la solmisation, la main syntonique que nous avons construite apporte son lot de contraintes supplémentaires. En effet, comme il existe, horizontalement, une distorsion de comma entre sol et ré, ces deux voix cessent d’être interchangeables comme c’était le cas dans la main pythagoricienne. Les problèmes rencontrés sont ici plus complexes, mais il est toujours possible de faire la liste des intervalles purs et de ceux qui ne le sont pas en comparant leurs voix extrêmes. La tierce mineure mi-sol, par exemple, est pure comme toutes les tierces incluses dans un seul hexacorde. Dans la main pythagoricienne, la tierce mi-ré, prise entre deux hexacordes adjacents, lui serait strictement équivalente. Ici, elle est trop petite d’un comma. D’autre part, une quinte ré-ré, où qu’on la prenne, sera toujours pure alors qu’une quinte sol-ré sera trop petite d’un comma.
Essayons de généraliser : nous avons vu que, indépendamment de l’hexacorde dans lequel on les prend, ut, fa et sol appartiennent à la série « + 1 » du labyrinthe de Barbour. On peut les qualifier de voix « élevées ». Ré, mi et la appartiennent à la série de base du labyrinthe. On les qualifiera, par opposition, de voix « abaissées ». On peut maintenant synthétiser les contraintes que le sintono fait peser sur la solmisation : les consonances dites parfaites, qui sont communes au diatono et au sintono, c’est-à-dire celles dont le rapport ne fait intervenir que des puissances de 2 et de 3 (unissons, quartes, quintes, octaves) doivent, pour être pures, se trouver entre deux voix du même groupe, c’est-à-dire entre deux voix élevées ou entre deux voix abaissées. Les consonances dites imparfaites, qui sont spécifiques du sintono, c’est-à-dire celles dont le rapport fait intervenir le facteur 5 (tierces et sixtes) ne peuvent se trouver entre deux voix du même groupe : pour les tierces et sixtes majeures, la note inférieure doit appartenir aux voix élevées et la note supérieure aux voix abaissées. Pour les tierces et sixtes mineures, la note inférieure doit appartenir aux voix abaissées et la note supérieure aux voix élevées.
S’il est susceptible de restreindre la liberté en matière de solmisation, l’usage de l’espèce sintono ne bouleverse en rien les principes de la méthode. L’élément nouveau est qu’à la même clef vont maintenant correspondre deux cordes, distantes d’un comma. Il ne s’agit que de la généralisation d’un principe déjà présent dans la main originelle où, à la même clef, peuvent correspondre deux cordes distantes d’un plein demi-ton (b mol et b dur). La nouveauté n’est donc que relative : les intervalles à éviter, tout simplement, deviennent plus nombreux et les chanteurs qui l’adopteraient doivent jongler davantage avec les voix. En fait, l’espèce sintono et la solmisation hexacordale s’accordent fort bien : le caractère modulaire du cristal fait que la partie vaut pour le tout. La description d’un seul hexacorde dans les rapports qu’il entretient avec ses voisins permet de rendre compte de manière unifiée de toutes les distorsions de comma, comme elle permet d’ailleurs de rendre compte de tous les demi-tons diatoniques. De plus, la redondance du système des voix permet à la solmisation, bien qu’elle n’ait selon toute vraisemblance pas été conçue à cette fin, de nommer tous les degrés, y compris ceux qui, surnuméraires par rapport au diatono, n’apparaissent que dans le sintono : les trois cordes qui se confondent en d sol-la-ré dans la première des deux espèces divergent dans la seconde en deux cordes distinctes d’un comma, qu’on peut appeler d sol pour la variante élevée et d la-ré pour la variante abaissée.
Zarlino a tout naturellement recours à une nomenclature de ce type pour la réponse qu’il fait, dans ses Sopplimenti46, aux critiques de Galilei. Dans un tableau analogue à celui de la figure 2.8, il met en regard la main guidonienne avec le grand système des Grecs, non plus cette fois-ci de l’espèce diatono, mais bien de l’espèce sintono (Figure 3.4). Tout en étant conscient du fait que ce système traditionnel est incomplet, il s’interdit d’y faire figurer des cordes supplémentaires. Le seul dédoublement de corde qu’il puisse donc prendre en compte est celui qui apparaît entre le tétracorde des conjointes et celui des disjointes, et qui correspond à la clef d. Comme on le voit, il attribue au d élevé les voix sol et ré, et à sa variante abaissée, auquel il réserve un d gothique, la voix la. Nous pouvons en tirer deux conclusions :
Le principe de l’attribution des voix de l’hexacorde à l’une ou à l’autre des variantes des cordes dédoublées en fonction de la configuration d’un hexacorde type, qui ressort implicitement des Istitutioni, se trouve confirmé explicitement par les Sopplimenti.
Comme les Istitutioni pouvaient le laisser supposer, Zarlino a ici choisi pour son hexacorde la séquence T-t-S-T-t. C’est cela qui l’amène à attribuer la voix ré à la variante élevée de la clef d alors que nous l’attribuons à la variante abaissée, comme le réclame la séquence t-T-S-T-t que nous avons retenue. L’application de la séquence de Zarlino n’aurait, sur le cristal syntonique, que des répercussions minimes : elle provoquerait le déplacement de toutes les distorsions de comma d’un hexacorde en direction dure, entre ré et la, alors qu’elles se trouvent chez nous entre sol et ré. A l’arrivée, les fréquences du labyrinthe de Barbour recrutées par le cristal seraient rigoureusement les mêmes : dans tous les cas, la totalité des hexacordes évoluent entre la série de base et la série « +1 » du labyrinthe. Le seul problème que provoque l’hexacorde choisi par Zarlino est d’ordre pratique : en son sein, la tierce ré-fa n’est pas pure et oblige donc le chanteur, pour obtenir le résultat sonore qu’il recherche – précisément une tierce pure – à aller chercher la bonne corde sur le la de l’hexacorde suivant. L’unique conséquence du choix de Zarlino est donc qu’il multiplie le nombre de muances nécessaires et qu’il rend plus complexe la liste des intervalles à éviter.
Quelle que soit donc la structure précise – celle de Zarlino ou la nôtre – choisie pour l’hexacorde et, par conséquent, pour le cristal, nous constatons que la solmisation hexacordale permet, en matière d’intonation juste, une souplesse qu’aucun solfège moderne n’est à même d’apporter.
En matière de diapason, le chanteur a cappella est comme l’homme qui croit marcher droit dans le désert : il aligne ses pas du mieux qu’il peut, mais sa trajectoire s’incurve inéluctablement. Sans la présence d’un repère, une boussole ou un sommet sur l’horizon, il lui est impossible de garder le cap.
Chercher à chanter juste, c’est approcher de très près les limites de l’audition, et surtout de la phonation humaines. Une voix, même la mieux exercée qui soit, fait des erreurs d’intonation dont, eu égard à la taille du comma, l’amplitude est importante. Un chanteur qui ne compterait que sur sa faculté de construire des intervalles de proche en proche, c’est-à-dire en ajustant chaque nouvelle note relativement à celle qui la précède immédiatement et à celle-là seulement, ce chanteur sans repère serait condamné, comme dérive le marcheur sans boussole, à détonner, par le seul jeu de ses erreurs successives. La présence d’un repère stable n’élimine pas les erreurs. Il permet seulement, au moment où elles deviennent perceptibles, de leur appliquer des compensations, de les minimiser et de faire en sorte que leur résultante soit nulle : le marcheur, ou le chanteur, arrive ainsi malgré elles à la destination qu’il s’était fixée.
Privé d’instruments, c’est sur sa mémoire que le chanteur devra compter pour « garder le cap ». Mémoire auditive, sûrement, mais aussi probablement mémoire « vocale » ou kinesthésique. Nous ne voulons pas dire que, pour chanter juste, un chanteur doive disposer de ce qu’on appelle « l’oreille absolue », c’est-à-dire la faculté de mémoriser à long terme des fréquences sonores. Beaucoup plus modestement, il doit pouvoir faire appel à une mémoire à court terme, réactivée périodiquement, par exemple aux cadences principales ou aux retours de la finale du mode, événements fréquents dans la musique de la Renaissance.
Les efforts considérables qui, des siècles durant, ont été consentis par tout chanteur pour mémoriser la main guidonienne avaient pour fonction de l’aider, justement, à se repérer : forcé de savoir en permanence sur quel degré de quel hexacorde il se trouvait et quelles muances lui étaient, à ce point donné, accessibles, un chanteur apprenti ne pouvait que mobiliser ses ressources en matière de mémorisation des fréquences. A cet égard, le modèle que nous a livré la théorie traditionnelle est sans équivoque : la main guidonienne, assortie d’autant d’hexacordes feints qu’on voudra, est bel et bien un système à diapason fixe. Par cela nous entendons qu’elle est ancrée dans une série de quintes pures donnée dont elle ne dévie pas. Autrement dit, toutes les muances imaginables se font sur une ligne horizontale du labyrinthe de Barbour : aucun glissement vertical n’est permis. La fréquence du la de l’hexacorde naturel, comme celle de n’importe quelle corde, caractérisée par sa position dans un hexacorde déterminé, ne varie pas.
Nous parlerions par contre de dérive du diapason lorsque, par le jeu d’erreurs d’intonation successives au cours d’une exécution particulière, une pièce se termine plus haut ou plus bas qu’elle n’a commencé, phénomène que tout chanteur ou groupe de chanteurs connaît bien, mais phénomène non reproductible et échappant aux constructions théoriques classiques. Le cas de telle pièce exceptionnelle47 qui, par le jeu de muances successives visant à éviter par exemple des tritons, se terminerait exactement un grand demi-ton pythagoricien (apotome) plus bas qu’elle n’avait commencé ne peut donc être assimilé à une dérive du diapason puisqu’il s’agit au contraire du résultat d’une excursion régulière quoiqu’extrême au sein même du système, sans fluctuation aucune due aux erreurs d’intonation.
Où ranger maintenant l’effet des distorsions de comma sur le diapason dans le cas où, ayant adopté une intonation fondée sur des consonances pures, tierces et sixtes comprises, l’on ferait prévaloir un principe de continuité comme celui de la note commune ? La dérive du diapason qui s’ensuivrait peut-elle être assimilée, ou seulement comparée à une excursion dans le domaine de la musica ficta, c’est-à-dire à un phénomène intervenant à l’intérieur d’un repère diatonique ? Certainement pas. Dans un système modulaire comme le grand système des Grecs ou la main guidonienne, l’espèce choisie (c’est-à-dire le principe d’intonation) influe sur l’organisation interne des modules (tétracordes ou hexacordes), mais en aucun cas sur leur position relative, c’est-à-dire sur les relations que, de degré à degré, ils entretiennent les uns avec les autres et qui constituent l’architecture générale du système. Cela signifie que, même si l’on puise, pour construire un module, dans deux séries de quintes du labyrinthe de Barbour, les muances continueront à se faire horizontalement, c’est-à-dire entre des modules qui sont distants les un des autres de quintes ou de quartes pures. Même adaptés au sintono, ces systèmes restent, dans le sens où nous l’entendons, à diapason fixe. En provoquant des mouvements obliques dans le labyrinthe de Barbour, l’application du principe de continuité rendrait donc caducs de tels repères.
Or, si le repère diatonique tombe, la voie s’ouvre inéluctablement à l’addition des erreurs d’intonation successives et à une dérive du diapason dont l’origine ne serait plus tant les distorsions de comma, mais bien plutôt l’imprécision du chanteur. Noyés dans cette dérive-là, les ajustements provoqués par les commas risquent bien de perdre toute signification. Voilà l’un des paradoxes auquel conduit le principe de continuité : pour que des chanteurs puissent le mettre en pratique, il faudrait qu’ils deviennent capables d’échapper à toute erreur d’intonation, c’est-à-dire à « calculer » leurs intervalles (commas compris), de proche en proche et de manière parfaitement exacte, ce qui est manifestement hors de portée de la physiologie humaine. Admettre, comme le font les tenants dudit principe, qu’un groupe de chanteurs qui rencontre une distorsion de comma est capable de modifier le diapason d’un comma exactement équivaut à prétendre que notre homme dans le désert, quoique privé de tout repère, est doué d’une mystérieuse faculté lui permettant de marcher de manière parfaitement rectiligne et que, par surcroît, lorsque son pied rencontre un caillou, il est capable d’infléchir sa trajectoire d’une minute d’angle exactement. C’est assez peu vraisemblable.
Nous postulons que le chanteur entraîné se construit un repère diatonique sur lequel il va s’efforcer d’aligner ses intervalles et qui aura pour effet de stabiliser le diapason. Jusqu’à quel point ce repère implicite peut-il coïncider avec un repère explicite comme la main guidonienne ? Y a-t-il eu, au cours de l’histoire, des groupes de chanteurs dont le repère implicite correspondait plus ou moins exactement avec le cristal syntonique ? Nous ne pouvons bien évidemment pas répondre à ces questions.
Le système de la main syntonique, assorti d’autant d’hexacordes feints qu’il est nécessaire, puise, comme nous l’avons vu, ses fréquences dans deux séries de quintes pures seulement. Ces deux séries seraient probablement suffisantes si toutes les notes feintes rencontrées dans la musique de la Renaissance correspondaient effectivement à des muances au sens plein du terme, c’est-à-dire à des excursions d’une certaine durée dans les hexacordes feints. Nous allons voir que cela n’est pas le cas.
Le moteur premier de ces excursions (qui correspondent à des mouvements horizontaux dans le labyrinthe de Barbour) est ce que certains théoriciens ont appelé la causa necessitatis48 : pour éviter un intervalle proscrit, par exemple un triton, soit vertical soit mélodique, un chanteur va changer d’hexacorde, le plus souvent en direction molle et donc éviter une quarte fa-mi en la remplaçant par une quarte fa-fa. Une fois le danger écarté et lorsque la mélodie le permettra, il pourra tranquillement revenir dans l’hexacorde de départ..
A la causa necessitatis, ces mêmes théoriciens opposent la causa pulchritudinis, dont la raison d’être n’est plus d’éviter tel ou tel intervalle, mais bien d’embellir les cadences, le plus souvent avec des mi, soit en gros ce que nous appelons aujourd’hui des sensibles et des tierces picardes. L’excursion se fait donc en direction dure, mais elle est aussi brève (une ou deux notes) que lointaine. Soit, dans une pièce portant un bémol à la clef, le squelette de cadence suivant :
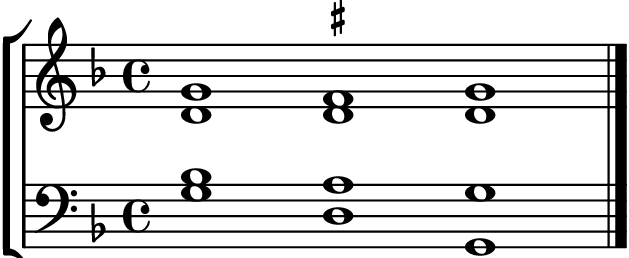
Figure 3.5 : Un squelette de cadence.
Dans la version « non embellie », en admettant qu’elle soit admissible, et en pythagoricien (Exemple 3.1), le soprano serait le plus probablement solmisé dans un hexacorde mol sur ré-ut-ré et le ténor sur fa-mi-ré. Le chanteur qui voudra embellir la cadence, c’est-à-dire transformer le ton mélodique du soprano en un demi-ton afin que, conformément aux règles usuelles, la sixte verticale A-F existant entre le soprano et le ténor devienne majeure, devra, s’il veut trouver un f mi approprié (c’est-à-dire un F#), sauter de trois hexacordes en direction dure et refaire aussitôt le saut inverse, ce qui est un exercice assez peu confortable. Au xvie siècle, les théoriciens rechignent en fait à considérer une telle sensible comme une le fruit d’une muance réelle et certains d’entre eux49 prescrivent qu’un motif G-F#-G soit solmisé comme s’il y avait un ton entier à la place du demi-ton : dans notre cas ré-ut-ré et non fa-mi-fa ainsi que l’exigerait en principe la présence de tout demi-ton.
Une telle recommandation prend une signification toute particulière dans un système diatonique fondé sur l’espèce sintono. En effet, le f-mi en question est non seulement lointain, il appartient en plus à la mauvaise série de quintes puisqu’il forme une sixte majeure pythagoricienne avec le A du ténor et une tierce majeure pythagoricienne avec le D de l’alto50, ce qui nuit à la pureté du second accord, comme on l’entend fort bien ici (Exemple 3.2). On pourrait tenter d’arranger les choses en demandant aux trois voix inférieures de faire en direction dure un saut de puce parallèle à celui du soprano et donc d’aller chercher un A sol et un D ut qui seraient un comma plus aigus que le A mi et le D ré. La solution, si elle n’est pas franchement choquante lorsqu’on l’écoute globalement (Exemple 3.3), est néanmoins peu satisfaisante car les demi-tons G-F# et Bb-A au soprano et au ténor, amputés d’un comma, sont pythagoriciens, le petit demi-ton cadentiel correspondant mal à l’esthétique de la Renaissance telle qu’en rend compte, par exemple, le tempérament mésotonique. Plus grave, le D de l’alto monte et redescend d’un comma au cours de ce petit motif et la quarte G-D à la basse est trop petite d’un comma.
Pour tenter de progresser, il nous faut maintenant nous référer à une remarque un peu sibylline de Galilei. Il signale que certains « contrapuntistes »51 ont l’habitude d’adjoindre à la note F un bécarre lorsqu’il est à la quinte de b mi et un dièse lorsque il fait une tierce majeure avec D, ceci pour signifier qu’avec le dièse, la quinte B-F# serait trop petite, et donc que le F marqué d’un dièse est légèrement plus grave – d’après ce qui précède dans la discussion de Gallilei, on comprend que la différence est d’un comma – que celui marqué d’un bécarre52. Cette remarque se révèle extrêmement éclairante si on la replace dans le contexte d’une cadence comme celle dont nous traitons ici :
Galilei, en adversaire de Zarlino et de l’intonation juste, considère comme aberrante cette distinction entre bécarre et dièse. Pour qu’il prenne la peine de la réfuter en détail, il faut donc qu’elle ait correspondu, de son temps, à une idée assez largement répandue, ce qui est la meilleure preuve que des praticiens du contrepoint ont bel et bien cherché des solutions en matière d’intonation juste.
Le F bécarre53, celui qui se trouve à la quinte de b-mi, est celui auquel on parvient par le jeu des muances, c’est-à-dire en parcourant les hexacordes feints et donc en obéissant à la causa necessitatis. C’est le f-mi qui, justement, fait problème dans notre cadence.
Pour que la distinction entre F# et F bécarre ait un sens, il faut que le D qui partage la quinte B-F bécarre (en une tierce mineure et une tierce majeure pures) soit situé un comma plus haut que celui qui soutient le F#. Dans le premier cas, il doit donc s’agir de la variante D sol et dans la seconde de la variante D la-ré de la main syntonique, que nous avons rattachées respectivement à la série « +1 » et à la série de base du labyrinthe de Barbour. Cela tend à montrer que les « contrapuntistes » en question évoluaient bel et bien dans un système diatonique sinon superposable, du moins analogue à notre cristal. Le D la-ré en question est celui qui, dans notre cadence, forme une quinte pure avec le G et une quarte pure avec le A.
Comme le F bécarre est un mi, il appartient à la série de base du labyrinthe de Barbour. Le F# fait donc partie de la série « -1 » et il est étranger au cristal syntonique. Son avantage est qu’il permet de respecter la causa pulchritudinis sans modifier la fréquence des notes qui auraient été utilisées dans la version « non embellie » de la cadence, c’est-à-dire avec la sixte mineure A-F et la tierce mineure D-F. Voici cette solution réalisée (Exemple 3.4) : non seulement, le demi-ton cadentiel y est un vrai demi-ton syntonique de 16/15, mais en plus le D reste stable et la quarte G-D est pure.
Le système diatonique simple dont nous étions parti ne recrutait ses fréquences que dans deux séries de quintes. Cela impliquait que toutes les tierces et sixtes majeures devaient avoir leur note inférieure dans la série « +1 » et que toutes les tierces et sixtes mineures devaient l’avoir dans la série de base. Les « contrapuntistes » cités par Galilei nous incitent maintenant à puiser, pour certaines de nos sensibles, dans la série « -1 », ce qui permet de transformer ponctuellement, le temps d’une cadence, une sixte mineure en sixte majeure ou une tierce majeure en tierce mineure sans avoir à changer la fréquence de leur note inférieure.
Il s’agit sans conteste d’un procédé fort commode, mais trouve-t-il sa place dans la théorie de Zarlino ? Oui : dans ce qu’il a nommé inspessatione, qu’on peut traduire par farcissure, et qui consiste à insérer dans une échelle diatonique (par exemple un tétracorde) une corde empruntée à une échelle chromatique. Soit un tétracorde chromatique (Figure 3.6) dans lequel, au demi-ton inférieur de 16/15 succède un demi-ton de 25/24, formant ensemble un ton mineur de 10/954. Inséré dans un hexacorde naturel, au-dessus de fa, son troisième degré correspond précisément au F# qu’utilisent les « contrapuntistes » de Galilei.

Figure 3.6 : Tétracorde chromatique, celon Zarlino.
Dans les Istitutioni, Zarlino ne donne guère de détails sur ces farcissures. Il y revient dans les Sopplimenti, lorsqu’il réfute les objections de Galilei. Il en insère même un certain nombre dans l’Istrumento accresciuto55 censé compléter (quoique de manière imparfaite) le sistema massimo afin de multiplier les intervalles purs. On y retrouve deux F# distants d’un comma, qui correspondent exactement au F bécarre et au F# cités par Galilei puisque le plus aigu des deux se trouve à la quinte pure de B et que le plus grave se trouve à la tierce majeure pure de la variante abaissée de D. Le premier appartient au système diatonique nucléaire et le second est une farcissure. Dans cet Istrumento accresciuto, on trouve même des farcissures pour Bb et Eb : un comma au-dessus de la variante diatonique, à laquelle on parvient par quintes successives à partir de F, Zarlino ajoute un Bb farci, qui se situe une tierce majeure pure en dessous de la variante abaissée de D, Le Eb farci étant lui-même une quinte pure en dessous du Bb farci.
De deux séries de quintes qu’il comptait au départ, notre modèle s’est quelque peu étendu. Entourant un noyau diatonique, représenté par notre cristal et recrutant ses fréquences dans la série de base et la série « +1 » du labyrinthe de Barbour exclusivement, nous avons maintenant quelques farcissures, qui font intervenir des fréquences tirées de la série « -1 » pour les dièses et de la série « +2 » pour les bémols. Le fait que Zarlino considère comme chromatiques des fréquences qui n’appartiennent pas aux deux séries de quintes du cristal syntonique montre qu’il était parfaitement conscient du caractère extra-diatonique de ces cordes. S’il avait admis, même implicitement, que le diapason puisse fluctuer librement au gré du principe de continuité, ou selon le bon vouloir des chanteurs, il n’aurait eu nul besoin de l’artifice des farcissures pour introduire ces cordes supplémentaires.
Nous pouvons maintenant formuler le seul choix qui s’offre aux « contrapuntistes » en matière d’intonation juste. Confrontés à une note feinte (en gros, ce que nous appelons une altération), ils devront choisir entre un traitement diatonique, c’est-à-dire une excursion dans les hexacordes du cristal, et un traitement chromatique, c’est-à-dire une farcissure. En règle générale, et si l’on se restreint au style le plus conventionnel de la Renaissance, un bémol, ou le bécarre qui l’annule obéissent à la causa necessitatis, ils appellent une excursion diatonique ; un dièse, notant une sensible ou une tierce picarde dans une cadence, obéit à la causa pulchritudinis et appelle une farcissure. Il y a bien sûr des cas limites, tout comme des styles qui tendent à faire éclater ce schéma simpliste, mais, en première approximation, il conduit, comme nous le verrons, à un modèle qui peut être appliqué de manière tout à fait mécanique.
Tentons finalement de résumer la nature de la controverse Zarlino-Galilei, dont les positions respectives ne sont peut-être pas aussi radicalement opposées que ne le laisse penser la vigueur de l’argumentation :
Zarlino relève les imperfections du système pythagoricien, et notamment son incapacité à fournir des tierces consonantes56. Partant de ce constat, il cherche quel système fournit des tierces majeures ou mineures pures et il les trouve dans le sintono de Ptolémée. Il préconise alors l’emploi, dans le chant a cappella exclusivement, de ces intervalles purs. Mais ce qu’il réclame est en fait à l’opposé du système dogmatique qu’on lui a, par la suite, imputé et qu’on lui impute encore :
A aucun moment, il ne prétend que les cinq tétracordes du sistema massimo de l’espèce sintono contiennent de manière exhaustive toutes les cordes nécessaires aux chanteurs. Il est trop bon mathématicien pour ne pas avoir remarqué que, ainsi limité, le système est largement insuffisant. Galilei lui-même, d’ailleurs, l’accuse d’avoir sciemment passé sous silence ces imperfections « stimando maggiormente (tirati da un’ambitioso & vano pensiero) l’impertinenti novità de capricci loro, che il comodo & utile che egli haverebbono possuto apportare al publico con ispiegarli la verità57 ». Au contraire, Zarlino a bien vu le parti qu’on peut tirer du comma pour les éviter58.
Il refuse, pour le chant, toute « participation », c’est-à-dire toute division du comma qui serait analogue à celle qu’on trouve dans les tempéraments instrumentaux. C’est l’un des seuls points où il se montre catégorique : tous les ajustements doivent se faire par commas entiers.
Il demande que les ajustements de commas ne s’entendent pas59, mais jamais il n’exige que tous les intervalles mélodiques sans exception soient purs, ce qui serait impossible à réaliser.
Il reste fidèle à l’architecture du système diatonique traditionnel, qui repose sur des modules (en théorie des tétracordes mais en pratique des hexacordes) qui se succèdent à intervalles de quartes et de quintes pures.
Lorsque, comme c’est le cas pour les instruments à clavier, les cordes utilisables sont en nombre limité, il admet la nécessité d’une « participation » du comma, et donc d’un tempérament, de préférence une variété du mésotonique. Il étend même cet usage au cas où des chanteurs sont accompagnés par des instruments60.
Ecrivant des années après son ancien maître dont la théorie s’est alors passablement répandue, à un moment où, par ailleurs, la polyphonie a cappella cède peu à peu du terrain devant la monodie accompagnée, Galilei se trompe souvent de cible : la plupart de ses critiques visent en effet l’attitude dogmatique qui n’est pas, nous venons de le voir, celle de Zarlino et qui consisterait à vouloir faire du sintono un système à sons fixes, c’est à dire sans cordes dédoublées61, attitude qui correspond grosso modo à celle des tenants d’une « gamme naturelle » comme celle de Helmholtz. Il lui est donc facile d’énumérer les intervalles faux qui sont inhérents à un tel système, et qui sont ceux-là mêmes qui rendraient inaudible un instrument à clavier ordinaire dont les touches blanches seraient accordées selon cette gamme. Il n’en partage pas moins les critiques que Zarlino fait au système pythagoricien, débouchant sur la nécessité de le modifier pour rendre les tierces et les sixtes sinon tout à fait pures, du moins consonantes. Ce n’est que sur l’application des inévitables compromis qu’il diverge partiellement de son ancien maître : pour les instruments à clavier, il préconise un tempérament mésotonique aux 2/7 de comma62, ce en quoi il ne fait que suivre Zarlino63. Pour la viole et le luth, il recommande ce qu’il identifie à l’incitato d’Aristoxène64, et qui ressemble à s’y méprendre au tempérament égal. Pour ce qui est du chant, il semble hésiter entre ces deux tempéraments65, avec une nette préférence pour le mésotonique, mais il ne parle jamais spécifiquement du chant a cappella. Le plus probable est que, dans son esprit, les chanteurs doivent s’adapter à l’indispensable instrument qui les accompagne.
Manifestement, les deux auteurs ne parlent pas de la même musique. Leur querelle est en fait un conflit de génération. L’idéal de Zarlino se trouve dans le passé : c’est la polyphonie d’un Willaert66, par essence vocale. Celui de Galilei est dans le futur : ce sont les recherches d’avant-garde de la camerata Bardi, avec comme aboutissement la monodie accompagnée et son corollaire, la basse continue, par essence instrumentale.
Le moment est enfin venu de mettre en pratique le modèle entrevu chez Zarlino, c’est-à-dire de tenter d’aligner des exemples musicaux tirés du répertoire sur les cordes du cristal syntonique, assorti des farcissures que nous venons de décrire.
Le premier exemple choisi sera simple : les seize accords d’un Crux fidelis entièrement homophone de Palestrina. C’est dans ce style que les problèmes d’intonation juste apparaissent le mieux, car ils ne sont parasités ni par des dissonances, ni par des notes de passage. Dans l’esprit de Zarlino, en effet, seules les consonances, parfaites et imparfaites, peuvent prétendre à la pureté. La question d’une dissonance pure, par exemple une septième, est absolument sans objet. C’est donc exclusivement dans les enchaînements de consonances que les problèmes de commas vont se poser de manière concrète.
Alors que bon nombre d’enchaînements contrapuntiques se font sans heurts et permettent de ménager des intervalles purs aussi bien verticalement (en simultanéité) qu’horizontalement (dans la mélodie) ou en oblique (entre deux voix différentes), il y a en a d’autres, en apparence tout aussi simples que les premiers, qui posent de délicats problèmes. Mais voyons déjà la pièce de Palestrina qui nous servira ici, et que nous commencerons par écouter en pythagoricien (Exemple 4.1) :

Figure 4.1 : Palestrina, Crux fidelis.
Essayons maintenant de « corriger » les tierces en déplaçant des notes individuelles d’un comma. Nous adoptons la méthode à la fois simple et mécanique qui nous semble correspondre le mieux à la théorie de Zarlino :
A l’exception des dièses cadentiels, nous évoluons à l’intérieur du repère diatonique que fournit le cristal syntonique. Cela signifie que nous faisons en sorte que toutes les tierces majeures aient leur note inférieure dans la série « +1 », leur note supérieure restant dans la série de base. Nous veillons aussi que toutes les tierces mineures aient leur note inférieure dans la série de base et leur note supérieure dans la série « +1 ». Nous ajoutons devant le corps des notes que nous plaçons dans la série « +1 » une demi-flèche ascendante. Nous renonçons à noter en toutes lettres les voix qui seraient celles d’une solmisation syntonique. Elles n’en sont pas moins présentes de manière implicite dans cette convention : les notes marquées d’une barre oblique recevraient obligatoirement une voix élevée (ut, fa ou sol), quand à celles de la série de base, elles appelleraient une voix abaissée (ré, mi ou la).
Pour les dièses apparaissant dans les cadences (sensibles et tierces picardes), nous avons recours à des farcissures, c’est-à-dire que nous laissons la note inférieure là où elle serait s’il n’y avait pas de dièse et que nous déplaçons la note altérée dans la série « -1 », ce que nous notons par une demi-flèche descendante.
Nous obtenons le résultat suivant, qu’on peut écouter ici (Exemple 4.2) et qui diffère de manière spectaculaire de la version pythagoricienne :

Figure 4.2 : La même pièce, avec corrections syntoniques.
Verticalement, toutes les quintes et toutes les tierces de cette pièce sont maintenant pures. Peut-on en dire autant si l’on considère les intervalles mélodiques ou obliques ? Cela serait trop beau : le cristal syntonique renferme, nous l’avons vu, des distorsions de comma. Il serait pour le moins étonnant que l’usage pratique les occulte totalement. Nous notons les anomalies suivantes (les chiffres renvoient à la numérotation des accords, les signes intercalaires seront explicités plus loin) :
2-3 et 5-6 : la quarte oblique formée par le D de la basse et le G du ténor est trop grande d’un comma.
9-10 : la tierce mineure G-Bb au ténor (ainsi qu’obliquement entre le ténor et la basse) est pythagoricienne. La quinte oblique G-D entre le ténor et l’alto est trop petite d’un comma.
13-14 : la quinte F-C à la basse (ainsi qu’obliquement entre la basse et l’alto) est trop petite d’un comma. La sixte majeure et la tierce mineure A-C, survenant obliquement entre le ténor et la basse d’une part, l’alto de l’autre, sont pythagoriciennes. L’unisson C-C à l’alto se traduit par la baisse d’un comma et la quarte oblique C-G entre l’alto et le ténor est trop grande d’un comma. Finalement, la quarte oblique F-C entre le soprano et l’alto d’une part, la basse de l’autre, est trop grande d’un comma.
14-15 : la tierce mineure et la sixte majeure C-A, survenant mélodiquement à l’alto et obliquement entre la basse et l’alto sont pythagoriciennes.
A l’oreille, ces distorsions ne sont guère perceptibles et, en tous les cas, ne sont pas de nature à compromettre l’effet intéressant qu’apporte la pureté verticale, ce d’autant plus que les autres enchaînements diatoniques se déroulent de manière parfaitement huilée. Quelques distorsions horizontales ou obliques semblent être le prix à payer pour qu’il soit possible de n’entendre que des accords purs. Le diapason, quant à lui, est globalement stable. Le recours à une farcissure pour la tierce picarde finale fait que la pièce se termine sur le G ré-la (donc G de la série de base) par laquelle elle commence. Un traitement diatonique de la cadence finale aboutirait à un G sol (donc un G de la série « +1 »). On peut se demander aussi, si le Eb de l’accord 14 ne pourrait pas être traité comme une farcissure. On voit en effet mal à quelle causa necessitatis il obéit. Dans ce cas, tout l’accord en question se retrouverait un comma plus haut, l’enchaînement 13-14 s’effectuerait sans heurts et, dans l’enchaînement 14-15, les tierces et sixtes deviendraient pures mais la quinte G-D serait trop petite d’un comma. L’important n’est pas tant, à notre avis, de choisir entre ces deux solutions que de prendre conscience de la signification d’un tel choix : dans un cas, un traitement diatonique avec alignement sur le repère que constitue le cristal syntonique, dans l’autre recours pour le Eb à une farcissure, donc à une note chromatique puisée dans la série « +2 », étrangère au repère diatonique.
Reste la question suivante : comment se fait-il que ces distorsions surviennent là et pas ailleurs ? Autrement dit, est-il possible de les classifier et de les prévoir ?
C’est une fois de plus l’abord hexacordal qui va nous permettre d’y voir clair. Mais avant cela, il nous faudra nous livrer à un travail fastidieux : dresser la liste de tous les enchaînements diatoniques possibles dans un système fondé sur le sintono.
Pour rendre la tâche réalisable, nous proposons de construire, sur les voix de l’hexacorde syntonique67, des sortes d’accords rudimentaires, que nous appellerons triplets. Par définition, un triplet se compose de trois voix. Ce qui distingue un triplet d’un accord est qu’il ne tient aucun compte des octaves et que, par conséquent, un accord et ses renversements correspondent à un seul et même triplet. La seule chose qui importe est que les trois voix du triplet puissent, si on les dispose correctement eu égard aux octaves, former une quinte pure, elle-même décomposée en deux tierces pures superposées. Par exemple, les voix ut-mi-sol d’un hexacorde formeront un triplet, de même que fa-la-ut, mais pas ré-mi-la. La voix de base du triplet, celle qui lui donnera son nom, sera celle qui se trouve à la base de la quinte. Dans les triplets ayant comme base une voix élevée (ut, fa, sol), la tierce inférieure sera majeure et l’on pourra parler de triplets majeurs. C’est une tierce mineure qui apparaîtra à la base des triplets formés sur une voix abaissée (ré, mi, la) et l’on pourra parler de triplets mineurs. Pour chaque hexacorde du cristal syntonique, il y a au maximum six triplets possibles, basés respectivement sur les six voix dudit hexacorde.
Une fois cela posé, il s’agit d’explorer systématiquement les successions de triplets possibles, afin de dresser la liste exhaustive des enchaînements diatoniques élémentaires présents dans la musique de la Renaissance et de repérer, pour chacun d’entre eux, s’ils entraînent ou non une distorsion de comma. Ces enchaînements constituent en quelque sorte le degré zéro du contrepoint. Ne tenant aucun compte, ni de la conduite des voix, ni des octaves, ils permettent de prévoir de manière exhaustive les intervalles horizontaux ou obliques qui sont susceptibles d’apparaître dans une composition homophone reposant, dans sa dimension verticale, sur des consonances pures et dont les notes sont alignées sur le cristal syntonique.
Il nous suffira, pour mener à bien notre classification des enchaînements diatoniques élémentaires, d’examiner le cas d’un hexacorde pris pour lui-même, puis dans ses rapports avec son ou ses voisins directs. La structure modulaire du cristal permet, rappelons-le, de généraliser au tout ce qui est valable en un point particulier. Les développements qui suivent n’apparaîtront clairs que si l’on garde sous les yeux, ou au moins en mémoire, le schéma du cristal syntonique.
Commençons par examiner ce qui se passe à l’intérieur d’un seul hexacorde. Il faut d’abord constater que toutes ses voix ne sont pas à même de fournir des triplets qui ne débordent pas dans un hexacorde adjacent. Ainsi, les triplets de mi et de sol auraient-ils besoin, pour être complets, d’un mi extra-hexacordal. Nous les laissons donc de côté pour l’instant et nous nous contentons de recenser les enchaînements possibles entre les quatre voix restantes, prises deux à deux. Cela conduit au tableau à double entrée suivant, où le premier triplet de l’enchaînement figure verticalement, le second horizontalement. Des seize cases possibles en théorie, on peut immédiatement retrancher les quatre qui forment la diagonale : un triplet qui se succède à lui-même ne constitue pas un enchaînement. De part et d’autre de cette diagonale, les deux parties du tableau s’organisent de façon symétrique et correspondent, par paires, à des enchaînements inverses. Il reste donc six paires d’enchaînements. Le + note la présence d’une distorsion de comma, le 0 son absence.
|
2e triplet 1e triplet |
ut | ré | fa | la |
| ut | + | 0 | 0 | |
| ré | + | 0 | 0 | |
| fa | 0 | 0 | 0 | |
| la | 0 | 0 | 0 |
L’enchaînement la-ut est superposable à l’enchaînement ré-fa, puisque tous deux reposent sur une tierce mineure pure et qu’on passe de l’un à l’autre par des lignes horizontales du cristal syntonique. Il en va de même de son inverse, ut-la, qui se confond avec fa-ré. La-ut et ut-la ne sauraient donc constituer des types à part entière. En définitive, on se retrouve avec cinq paires de types intra-hexacordaux que nous désignons ci-après par l’initiale des voix de base de leurs triplets respectifs, en minuscules (par exemple, ur pour ut-ré). Sur ces deux fois cinq types, une seule paire, ur/ru, contient une distorsion de comma. L’enchaînement construit sur les triplets ut et ré est en effet le seul à contenir les deux voix ré et sol qui forment une quarte trop grande d’un comma, unique consonance de l’hexacorde syntonique à ne pas être pure. Cette distorsion de comma intra-hexacordale, que nous noterons désormais par le signe +, apparaît à deux reprises dans le Crux fidelis de Palestrina (2-3 et 5-6).
Comme il n’a jusqu’ici pas été tenu compte des octaves, chacun de ces types peut, lorsqu’il apparaît dans une composition musicale, se traduire par deux mouvements de la note de base, l’un ascendant, l’autre descendant de l’intervalle complémentaire. Dans le tableau ci-dessous, on trouvera la liste de ces types, avec, pour chacun d’entre eux, le mouvement ascendant et le mouvement descendant auxquels il correspond.
| Mouvement ascendant | Mouvement descendant | ||
|---|---|---|---|
| ur | ton mineur | septième (9/5) | Types entraînant une distorsion de comma intra-hexacordale (+) |
| ru | septième (9/5) | ton mineur | |
| uf | quarte (entre voix élevées) | quinte | Types n’entraînant pas de distorsion de comma |
| fu | quinte (entre voix élevées) | quarte | |
| rf (=lu) | tierce mineure | sixte majeure | |
| fr (=ul) | sixte majeure | tierce mineure | |
| rl | quinte (entre voix abaissées) | quarte | |
| lr | quarte (entre voix abaissées) | quinte | |
| fl | tierce majeure | sixte mineure | |
| lf | sixte mineure | tierce majeure |
Abordons maintenant les enchaînements survenant entre des triplets pris dans deux hexacordes adjacents. Pour commencer, nous construirons un tableau à double entrée dans lequel on trouvera, verticalement, la voix de base du triplet de départ et, horizontalement, celle du triplet d’arrivée, pris dans un hexacorde adjacent en allant du dur vers le mol. Il nous faudra cette fois-ci prendre en compte les triplets construits sur les six voix de chacun des hexacordes, d’où un tableau à trente-six cases. Les enchaînements UT-SOL, RE-LA, FA-UT et LA-MI peuvent être ignorés car ils correspondent à la répétition du même triplet. D’autres parmi ces enchaînements inter-hexacordaux peuvent être réduits à l’un des enchaînements intra-hexacordaux décrits plus haut. Par exemple, l’enchaînement UT-UT pris entre deux hexacordes adjacents est superposable au type uf intra-hexacordal : tous deux sont basés sur deux voix élevées distantes d’une quarte pure et toutes leurs voix respectives communiquent entre elles par des lignes horizontales du cristal syntonique. Nous indiquons, dans les cas analogues, le type intra-hexacordal correspondant. Pour les autres enchaînements, ceux qui sont réellement inter-hexacordaux, nous notons le signe * lorsqu’il y a une distorsion de comma et 0 lorsqu’il n’y en a pas.
|
mol dur |
UT | RE | MI | FA | SOL | LA |
| UT | uf | ∗ | fr | ∗ | ur | |
| RE | rf | lr | rl | lf | ru | |
| MI | 0 | ∗ | lr | ∗ | lf | ∗ |
| FA | ur | fl | uf | fu | fr | |
| SOL | ∗ | ∗ | ur | ∗ | uf | ∗ |
| LA | lf | ∗ | 0 | rf | lr |
En se déplaçant, non plus du dur vers le mol, mais du mol vers le dur, on obtient le tableau suivant, miroir du premier :
|
dur mol |
UT | RE | MI | FA | SOL | LA |
| UT | fu | fr | 0 | ∗ | fl | |
| RE | ∗ | rl | ∗ | ru | ∗ | ∗ |
| MI | rf | lr | rl | lf | ru | |
| FA | ∗ | fl | ∗ | fu | ∗ | 0 |
| SOL | ur | fl | uf | fu | fr | |
| LA | ru | ∗ | rf | ∗ | rl |
Examinons en détail l’un de ces enchaînements inter-hexacordaux, par exemple MI-LA, en fixant le triplet de départ dans un hexacorde naturel et celui d’arrivée dans un hexacorde mol et en représentant chaque triplet verticalement. On a :
B mi A mi
G sol F ut
E mi D la
La tierce mineure B mi-D la est ici pythagoricienne puisque ses deux voix, abaissées, appartiennent à la série de base. La quarte G sol-D la est trop grande d’un comma puisque ses deux voix n’appartiennent pas à la même série de quintes. On peut répéter le même exercice pour tous les enchaînements marqués d’un astérisque, de manière à dresser, pour chacun d’entre eux, la liste des consonances qui subissent la distorsion de comma.
Chacun des deux tableaux ci-dessus contient douze enchaînement inter-hexacordaux proprement dits dont la plupart renferment une distorsion de comma, c’est-à-dire qu’ils font apparaître au moins une consonance horizontale ou oblique trop petite ou trop grande d’un comma. Mais ces deux fois douze enchaînements sont eux-mêmes réductibles à un nombre plus restreint de types. En effet, si l’on s’intéresse pour l’instant tableau qui va du dur vers le mol, il apparaît que l’enchaînement SOL-LA est superposable à l’enchaînement UT-RE : leur triplet de départ est basé sur une voix élevée et leur triplet d’arrivée sur une voix abaissée, toutes deux distantes d’une quinte (trop petite d’un comma). On passe d’ailleurs de l’une à l’autre en suivant les lignes horizontales du cristal syntonique. Des considérations analogues permettent de réduire SOL-UT à UT-FA, LA-RE à MI-LA et LA-FA à MI-UT, et d’opérer de telles réduction pour le tableau qui va du mol vers le dur. Il reste en fin de compte huit paires de types inter-hexacordaux, dont nous rendons compte par les initiales de leurs triplets, en majuscules pour les distinguer des enchaînements intra-hexacordaux.
| Mouvement ascendant | Mouvement descendant | ||
|---|---|---|---|
| Hexacordes adjacents en allant du dur vers le mol | |||
| UR (=SL) | Quinte - comma | Quarte + comma | Types entraînant une distorsion de comma inter-hexacordale (∗) |
| UF (=SU) | Septième mineure pythagoricienne | Ton majeur (entre voix élevées) | |
| MR | Tierce mineure pythagoricienne | Sixte majeure pythagoricienne | |
| ML (=LR) | Septième mineure pythagoricienne | Ton majeur (entre voix abaissées) | |
| SF | Tierce mineure pythagoricienne | Sixte majeure pythagoricienne | |
| MF | Quinte diminuée | Triton | |
| SR | Octave - comma | Comma | |
| MU (=LF) | Demi-ton syntonique | Septième majeure syntonique | Type n’entraînant pas de distorsion de comma inter-hexacordale |
| Hexacordes adjacents en allant du mol vers le dur | |||
| RU (=LS) | Quarte + comma | Quinte - comma | Types entraînant une distorsion de comma inter-hexacordale (∗) |
| FU (=US) | Ton majeur (entre voix élevées) | Septième mineure pythagoricienne | |
| RM | Sixte majeure pythagoricienne | Tierce mineure pythagoricienne | |
| LM (=RL) | Ton majeur (entre voix abaissées) | Septième mineur pythagoricienne | |
| FS | Sixte majeure pythagoricienne | Tierce mineure pythagoricienne | |
| FM | Triton | Quinte diminuée | |
| RS | Comma | Octave - comma | |
| UM (=FL) | Septième majeure syntonique | Demi-ton syntonique | Type n’entraînant pas de distorsion de comma inter-hexacordale |
Ces huit paires ne se rencontrent évidemment pas avec la même fréquence dans la musique de la Renaissance. Par exemple, la paire MF/FM, qui consiste en un mouvement de triton, entrerait le plus souvant en contradiction avec les règles du contrepoint. La paire SR/RS, dans laquelle se succèdent un accord majeur et un accord mineur distants d’un comma ne devrait pas, non plus se rencontrer couramment.
Il y a trois distorsions de comma inter-hexacordales (nous utilisons l’astérisque pour les signaler) dans le Crux fidelis de Palestrina, qui, comme on peut s’y attendre, se trouvent bien où nous avions précédemment décrit des intervalles problématiques : 9-10 est du type UF, 13-14 du type UR et 14-15 du type LM (on fait abstraction du F# farci de 15).
L’associations des distorsions de comma avec des types d’enchaînements diatoniques pourrait être anecdotique si elle ne mettait en évidence quelques caractéristiques importantes du système diatonique bâti sur le sintono.
Tout d’abord, et à une exception près (la paire ur/ru), les enchaînements intra-hexacordaux sont exempts de distorsion de comma. La seule qui s’y glisse a peu de conséquences puisqu’elle ne peut toucher qu’une seule consonance (la quarte ré-sol). A une exception près également (la paire MU/UM, qui est fort rare dans la pratique), les enchaînements inter-hexacordaux présentent tous une distorsion de comma, plus importante que la distorsion intra-hexacordale puisqu’elle peut toucher simultanément plusieurs consonances horizontales ou obliques, et notamment des tierces et des sixtes. Les types intra-hexacordaux se distinguent donc assez radicalement des types inter-hexacordaux et, par conséquent aussi, l’unique distorsion intra-hexacordale des sept distorsions inter-hexacordales.
Il faut rappeler ensuite que l’hexacorde est le plus grand module diatonique possible qui soit exempt de toute consonance parfaite diminuée ou augmentée. L’ajout d’un septième degré ne peut qu’introduire un tel intervalle. Ainsi donc, chaque enchaînement diatonique débordant le cadre d’un seul hexacorde doit nécessairement renfermer une fausse relation68. A l’exception de la paire SR/RS, qui contient une fausse relation d’octave, tous les enchaînements inter-hexacordaux contiennent ce qui, en pratique, se traduira presque toujours par une quinte ou une quarte mi-fa, c’est-à-dire une fausse relation de triton ou de quinte diminuée. Pour mettre immédiatement le doigt sur toutes les distorsions de comma inter-hexacordales d’une pièce musicale, il suffit donc d’y repérer les fausses relations qui, en vertu des règles usuelles du contrepoint, surviendront avant tout obliquement. Voilà un outil de prévision extrêmement puissant.
Un mot encore à propos des farcissures cadentielles. Comme on peut le constater chez Palestrina, elles s’accompagnent souvent aussi, obliquement, par des fausses relations, mais elles évitent en général les distorsions de comma qu’entraînerait un traitement diatonique. Celle de l’accord 7, par exemple, si on la considérait comme pleinement diatonique, et qu’on élevait en conséquence l’accord d’un comma, correspondrait à une excursion trop lointaine pour que l’enchaînement 6-7 puisse être réduit à un type élémentaire. On pourrait toutefois en rendre compte en le décomposant en deux enchaînements successifs, le premier, intra-hexacordal, de type rl et le second, inter-hexacordal, de type RS. Cette solution diatonique accumule les handicaps vis à vis de la farcissure chromatique.
Etrangères au repère diatonique, les farcissures ne font que se substituer de manière superficielle et momentanée à une note diatonique non altérée – dans le cas de l’accord 7, un C naturel – qui reste en quelque sorte présente de manière sous-jacente, et continue à gouverner l’alignement sur le repère diatonique : avec ou sans farcissure, l’enchaînement 6-7 est et demeure un type rl intra-hexacordal.
Les farcissures sont des embellissements de courte durée qui ne touchent que la voix dans laquelle elles apparaissent et ne modifient en rien le comportement des autres voix. Elles se comportent comme des parenthèses et sont acceptables à condition qu’on les referme aussitôt après les avoir ouvertes, raison pour laquelle nous les avons notées par le double signe < >. En pratique, elles sont de la seule compétence de la voix qui les porte : que le chanteur concerné décide d’élever ou non une note cadentielle, l’intonation des autres chanteurs ne sera en rien modifiée. Par comparaison, une muance obéissant à la causa necessitatis devra se négocier entre tous les chanteurs : un déplacement au sein du cristal diatonique aura des répercussions sur plusieurs voix.
A deux reprises, déjà, nous nous sommes trouvé confronté à la notion de principe de continuité :
Lorsque, en préambule, nous avons examiné le God save the King traité par Barbour et que nous avons remis en question la validité de la méthode consistant à s’appuyer sur la note commune pour régler des enchaînements d’accords.
Lorsque, au moyen de l’image du marcheur dans le désert nous avons mis en évidence l’antinomie existant entre, d’une part, la notion de repère diatonique, telle qu’elle apparaît en filigrane dans la théorie musicale de la Renaissance et, d’autre part celle d’un principe de continuité qui consisterait à faire se succéder, de proche en proche, le plus de consonances pures possibles sans se soucier d’un quelconque repère. L’antinomie en question se traduit de manière très concrète : l’alignement sur un repère diatonique stabilise le diapason alors que le principe de continuité amène des fluctuations et, potentiellement, une dérive de celui-ci.
Nous nous proposons de réexaminer les rapports entre principe d’alignement (sur un repère diatonique qui, pour nous, sera le cristal syntonique) et principe de continuité, à la lumière des types d’enchaînements diatoniques que nous venons de mettre en évidence. L’exemple suivant nous servira de support, tiré de la fameuse chanson Bon jour mon cœur, de Roland de Lassus dont on peut écouter, pour commencer, la version pythagoricienne (Exemple 4.3) :

Figure 4.3 : Roland de Lassus, extrait de Bonjour mon cœur.
Un examen sommaire de cet extrait va nous permettre, tout d’abord, de désigner comme farcissures les dièses figurants aux accords 3, 5, 15 et 17-18 (ce choix comporte bien sûr une part d’arbitraire). Ensuite, nous pouvons localiser les enchaînements inter-hexacordaux susceptibles d’entraîner des distorsions de comma en recherchant les tritons ou les quintes diminuées obliques. Nous en trouvons pas moins de cinq, de type RU (1-2), LM (4-5, 12-13, 16-17) et FU (7-8). Nous repérons aussi un enchaînement intra-hexacordal de type ur (2-3). Les enchaînements restants sont intra-hexacordaux et exempts de toute distorsion. Comme toutes leurs consonances, verticales, horizontales et obliques sont pures, ils ne sauraient provoquer de conflit entre le principe d’alignement et le principe de continuité.
Le cas de l’enchaînement ur (2-3) se règle facilement : si l’on désirait corriger la quarte oblique D-A, trop grande, apparaissant entre le ténor et la basse, on ferait en même temps de la tierce mineure mélodique à l’alto une tierce pythagoricienne et l’on raccourcirait la quinte oblique B-E entre le soprano et l’alto. Le remède serait pire que le mal et l’on peut gager que les tenants du principe de continuité choisiraient, tout bien pesé, la solution dictée par le principe d’alignement, celle qui sacrifie la quarte D-A. Ce sont bel et bien les enchaînements inter-hexacordaux qui, seuls, mettent en conflit principe d’alignement et principe de continuité. Essayons tout d’abord de donner une version de notre exemple qui suive le principe de continuité, en rendant pures les tierces mélodiques F-D (1-2, 7-8, 12-3 au ténor), D-B (4-5 au ténor) et G-E (16-17). On peut l’entendre ici (Exemple 4.4), avec le dernier accord répété au diapason de départ. Tous les accords sont parfaitement purs, de même que toutes les consonances horizontales, mais l’effet sonore est désastreux : la chute de cinq commas correspond à un bon demi-ton et le moins qu’on puisse dire est qu’elle s’entend. Pourra-t-on encore, après écoute, défendre le principe de continuité ?
Ecoutons maintenant une version alignée sur le repère diatonique que constitue le cristal syntonique et qui, farcissures mises à part, est donc limitée aux séries de base et « +1 » du labyrinthe de Barbour (Exemple 4.5) :

Figure 4.4 : La même pièce, avec corrections syntoniques.
Ici aussi, tous les accords sont purs. Le principe d’alignement garantit la stabilité du diapason, avec pour inévitable conséquence que les tierces mélodiques ci-dessus mentionnées sont pythagoriciennes. Malgré ces distorsions, on se reprend à croire à l’intonation juste.
Bien sûr, toutes les pièces polyphoniques ne recèlent pas cinq enchaînements inter-hexacordaux en dix-huit accords. Tous les enchaînements inter-hexacordaux ne poussent pas non plus à la baisse du diapason lorsqu’on leur applique le principe de continuité : seuls ceux qui vont du mol au dur ont cet effet. Ceux qui vont du dur au mol, en revanche, poussent à la hausse et le hasard peut faire que les uns compensent les autres. Mais rien n’oblige qu’une telle compensation se produise effectivement : contrairement aux farcissures, qui impliquent une compensation immédiate, les enchaînements inter-hexacordaux sont des phénomènes isolés. Le style de Bon jour mon cœur n’a rien d’extraordinaire ou d’osé et les successions d’enchaînements qu’il recèle peuvent se produire dans n’importe quelle pièce. Le fait est que ce sont les enchaînements inter-hexacordaux qui, seuls, font la différence entre principe de continuité et principe d’alignement. Lorsqu’ils s’accumulent, le principe de continuité donne un résultat catastrophique.
Même appliqué avec la plus grande des rigueurs, le principe de continuité, il faut le souligner, ne parviendrait pas à sauver toutes les consonances, verticales, horizontales et obliques. Plusieurs quartes obliques trop grandes persisteraient dans la version de Bon jour mon cœur à laquelle il conduit : A-E (4-5 entre le soprano et la basse), C-G (7-8 et 12-3 entre le soprano et l’octave alto-basse) et D-A (16-17 entre l’alto et l’octave soprano-basse). En définitive, la seule mesures qui aurait pu satisfaire les tenants du principe de continuité, s’ils ont existé à la Renaissance, aurait été d’interdire aux compositeurs tout enchaînement inter-hexacordal ou, en d’autres termes, de proscrire toute fausse relation de triton, de quinte augmentée ou d’octave, qu’elle soit verticale, horizontale ou oblique. On sait bien qu’une telle musique n’a jamais constitué un style. On peut se demander toutefois si Zarlino, lorsqu’il prescrit – en quoi il est particulièrement sévère – de « fuir de telles relations »69 dans le contrepoint à deux parties, n’est pas sensible, quoiqu’il ne le dise pas expressément, aux problèmes qu’elles posent en termes d’intonation. Le fait que, avant et après lui, les compositeurs n’aient jamais banni ces fausses relations de leurs compositions polyphoniques est un signe : si l’on admet que l’intonation juste a pu être activement et consciemment recherchée par des chanteurs à la Renaissance, on doit aussi admettre qu’ils n’étaient nullement guidés par le principe de continuité.
Nous n’aurions pas de nous-même pris un exemple chez Josquin : de deux générations plus âgés que Zarlino, le grand franco-flamand et ses premiers interprètes ne sauraient avoir été influencés par des élaborations théoriques sur le sintono. Il n’en demeure pas moins que les œuvres de Josquin ont été copiées, publiées et chantées très longtemps après sa mort. Il est donc fort possible qu’elles aient été, au cours du xvie siècle, interprétées par des disciples de Zarlino. Il est en outre important de souligner qu’aucun musicien de la Renaissance (à part, peut-être, Zarlino lui-même s’il a activement cherché à éviter toute fausse relation70) n’a jamais écrit en pensant aux distorsions de comma qu’il introduisait dans ses compositions. Les choix en matière d’intonation sont et restent du ressort, conscient ou inconscient, de l’interprète. Même s’ils n’avaient, par la force des choses, pas lu Zarlino, les chanteurs contemporains de Josquin ont pu, plus ou moins consciemment, s’essayer à adoucir les tierces pythagoriciennes qu’ils auraient dû, selon la théorie qu’ils connaissaient, chanter. Il n’est donc pas complètement aberrant d’analyser un fragment de Josquin à dans l’optique de l’intonation juste.
De fait, quelques mesures du motet Ave Maria de Josquin ont fait l’objet, il y a peu, d’un débat nourri qui, parti d’un problème de musica ficta71, a débouché sur la question de l’intonation juste, et en particulier sur une défense de celle-ci signée Jonathan Walker72. Il nous semble intéressant de donner à entendre les solutions proposées dans cet article, tout en les soumettant à notre analyse de la question.
La première version de cet extrait comprend les altérations éditoriales proposées par Roger Wibberley. La voici, ainsi que sa réalisation en pythagoricien (Exemple 4.6) :

Figure 4.5 : Un fragment du motet Ave Maria de Josquin, avec les altérations éditoriales de Wibberley.
Le passage ne comporte a priori aucune note qu’on puisse qualifier de farcissure (les sources originales ne comportent d’ailleurs quasiment pas d’altérations notées), on lui appliquera donc un traitement pleinement diatonique. On trouve six fausses relations de triton (ou de quinte diminuée), qui signalent autant d’enchaînements inter-hexacordaux : au milieu de la mesure 45 (type RU), entre les mesures 46 et 47 (type RU73), entre les mesures 48 et 49 (type LM74), entre les mesures 49 et 50 (type RU), entre les troisième et quatrième minimes de la mesure 51 (type RM75) et au milieu de la mesure 52 (type FU). Tous vont du mol au dur, on peut donc prévoir que l’application du principe de continuité fera baisser le diapason de six commas76. L’audition du résultat (Exemple 4.7) n’est pas de nature à nous réconcilier avec ledit principe.
Walker fait des suggestions assez radicalement différentes. Il a bien vu que le principe de continuité ne produisait pas un résultat satisfaisant et il s’applique, quoiqu’il ne le formule pas de manière claire, à rester aligné sur un repère diatonique : en fait la trop fameuse gamme de Helmholtz qui apparaît en grisé sur sa figure 1, à laquelle il ajoute le D de la série de base ainsi que le Bb de la série « +1 » signalés tous deux par le signe « - » (on peut voir ici la réalisation originale de Walker). La gamme de Helmholtz avec D dédoublé correspond à la superposition des deux hexacordes syntoniques naturel et dur. Il n’est donc pas étonnant qu’un tel repère fonctionne bien tant que la musique reste limitée auxdits hexacordes, c’est-à-dire jusqu’à la fin de la mesure 47. Le passage dans l’hexacorde mol rendrait nécessaire l’emploi du G ré, qui appartient à la série de base. Walker ne semble pas s’en être avisé et il continue à utiliser le seul G de la série « +1 », ce qui nuit de manière perceptible au résultat sonore, notamment à la mesure 49 et, quoique très brièvement, à la mesure 51. On peut entendre ici (Exemple 4.8) sa solution. Pour plus de clarté, nous la retranscrivons dans notre notation, en soulignant d’un trianble les G litigieux :

Figure 4.6 : La solution de Walker (version Wibberley).
L’alignement sur le cristal syntonique produit quasiment le même résultat. Seule différence : lorsque le chant se déplace dans l’hexacorde mol (depuis la dernière minime de la mesure 48 jusqu’à la fin de 49, puis pour les trois premières minimes de la mesure 51), elle a recours à des G de la série de base et non à ceux de la série « +1 » tels que suggérés par Walker. On peut l’entendre ici (Exemple 4.9). Ces deux solutions presque superposables sont toutes deux alignées sur un repère diatonique et, par conséquent, la dérive du diapason, inhérente au principe de continuité, ne se produit pas. Leur seule divergence, à notre avis, tient au fait que Walker, dans le repère qu’il utilise (pour l’octave C-C, la séquence T-t-S-T-t-T-S), reste malgré lui prisonnier de la rigidité d’une gamme, là où seul la souplesse d’un système modulaire conduit à un résultat réellement probant.
On notera les deux glissandos de comma qui apparaissent au ténor sur les D des mesures 45 et 46-47. L’alignement sur le cristal syntonique en génère un de plus, toujours au ténor, sur le G des mesures 49-50. Ces micro-ajustements sont plutôt anecdotiques : ils se produisent lorsqu’une note est tenue par dessus un enchaînement inter-hexacordal. Si l’on admet que les voix qui « bougent » s’alignent sur le repère diatonique, il n’y a aucune raison de ne pas admettre que la tenue puisse faire de même.
Voici maintenant les altérations éditoriales proposées par Margaret Bent, qu’on écoutera tout d’abord en pythagoricien (Exemple 4.10) :

Figure 4.7 : La version Bent.
Le but premier de l’éditeur est d’éviter les tritons. On pourrait donc s’attendre à ce que les fausses relations s’y trouvent en moins grand nombre que dans la version Wibberley. Il n’en est rien. L’excursion dans le domaine de la musica ficta ne fait que les déplacer. Jusqu’à la mesure 48, la version Bent est superposable à la version Wibberley et comporte donc les deux enchaînements inter-hexacordaux déjà mentionnés. Celui qui apparaissait entre les mesures 48 et 49 est remplacé, du fait du recours à Eb et à Ab, par un simple type lr intra-hexacordal, mais une nouvelle fausse relation apparaît au milieu de la mesure 49, révélant un type RU inter-hexacordal. De manière analogue, celui qu’on trouvait entre les mesures 49 et 50 fait place également à un type lr intra-hexacordal, mais, à nouveau, un type RU inter-hexacordal surgit entre les mesures 50 et 51. L’avant-dernière distorsion, qu’on trouvait dans l’édition Wibberley entre la troisième et la quatrième minime de 51, fait place à un type lf intra-hexacordal, mais il en réapparaît une, de type RS inter-hexacordal, entre la deuxième et la troisième minime de 52, qui se superpose au type FU qu’on trouvait déjà chez Wibberley, sans pour autant le faire disparaître. Ce dernier enchaînement a la particularité de représenter un saut de quatre hexacordes en direction dure77. Il recèle deux fausses relations, de triton et de quinte diminuée, entre le F de la basse et le B du soprano, entre le Ab de l’alto et le D du ténor. Un tel enchaînement, si on lui applique le principe de continuité, provoque à lui seul une chute du diapason de deux commas. On peut entendre ici (Exemple 4.11) la version Bent réalisée selon le principe de continuité.
Walker propose, pour cette version, deux solutions. Les originaux peuvent être consultés ici et là. Nous reproduisons ci-dessous la première en utilisant notre notation (les demi-flèches ascendantes avec double pointe désignent des notes de la série « +2 »), accompagnée de sa réalisation sonore (Exemple 4.12) :

Figure 4.8 : Première solution de Walker (version Bent).
Voici la seconde, ainsi que sa réalisation sonore (Exemple 4.13) :

Figure 4.9 : Seconde solution de Walker (version Bent).
En fait, ces deux solutions diffèrent fort peu. A l’exception du D de la mesure 49, qui n’est manifestement pas accordé dans la première (il s’agit probablement d’une erreur), tout se joue au début de la mesure 48 où la solution 1 « s’envole » d’un comma et occupe donc les séries « +1 » et « +2 », alors que la solution 2 continue – normalement, dirions-nous – à évoluer entre la série de base et la série « +1 ». On comprend mal cet écart de la solution 1 : il se produit sur un simple type uf intra-hexacordal et aucune distorsion de comma ne peut l’expliquer. Sa seule justification semble être la volonté de faire que l’extrait se termine au diapason où il a commencé. Pour les deux enchaînements inter-hexacordaux suivants, et dans ses deux solutions, Walker s’applique à maintenir le diapason, en contradiction avec le principe de continuité, ce qui se traduit par deux glissandos de comma aux mesures 49 et 50-51. Le dernier point problématique est l’enchaînement des deuxième et troisième minimes de 52. Dans ses deux solutions, Walker limite à cet endroit la chute du diapason à un seul comma, au lieu des deux qu’il obtiendrait en appliquant mécaniquement le principe de continuité. Il perd donc un comma en route, et c’est pour cela que sa solution 2 se termine un comma plus bas qu’elle n’a commencé, alors que sa solution 1, qui comprend un ajustement arbitraire et préventif vers le haut entre 47 et 48, se termine au diapason.
L’alignement sur le cristal syntonique conduit à une solution qui, jusqu’à la deuxième minime de 52, est superposable à la solution 2 de Walker. Pour les deux derniers accords, elle correspond à sa solution 1. C’est logique : dans ses deux solutions, Walker perd un comma avant les deux derniers accords, perte que l’élévation précoce de sa solution 1 prévient. Voici cette dernière solution, qu’on peut entendre ici (Exemple 4.14) :

Figure 4.10 : Alignement sur le cristal syntonique (version Bent).
On le voit, les solutions auxquelles parvient Walker sont, de manière générale fort éloignées de celles auxquelles conduit le principe de continuité. Elles sont en revanche extrêmement proches de celles que produit l’alignement sur le cristal syntonique. Walker justifie ses propres solutions comme une application « pragmatique, flexible et ad hoc » des principes de l’intonation juste, qu’il oppose au « modèle rigide et dogmatique » qui provoquerait une dérive du diapason78. Soit… Mais il prétend aussi fournir un « modèle théorique79 ». Or, à notre sens, un bon modèle doit pouvoir fonctionner, une fois posées les conditions de départ, avec le moins possible d’interventions volontaires, et si possible pas du tout. Il n’est donc en soi nullement dogmatique d’appliquer un modèle de manière rigide : c’est la seule manière de le mettre à l’épreuve. A ce titre, le modèle fondé sur le principe de continuité est un bon modèle. Appliqué de manière mécanique, il produit un résultat aisément prévisible et reproductible, notamment en ce qui concerne les fluctuations du diapason. Ce résultat, à son tour, permet de conclure à l’inadéquation du modèle. Prétendre opposer à un modèle inadéquat, non pas un modèle plus adéquat, mais ce même modèle appliqué de manière moins rigide est, d’un point de vue théorique, faible : des interventions ad hoc, et donc non gouvernées par un principe général ou des exceptions formellement définies, ne sauraient constituer un modèle, et N. Meeus80 a beau jeu de le relever.
Ce que nous voulons faire valoir ici, c’est que le principe de continuité n’est qu’un modèle d’intonation juste en face d’un ou peut-être plusieurs autres possibles. Le principe d’alignement constitue un modèle alternatif qui, appliqué tout ce qu’il y a de plus mécaniquement, conduit à un résultat quasiment identique (nous serions tenté d’affirmer qu’il est légèrement meilleur) à celui qu’atteint Walter par des « procédures flexibles » qu’il peine à expliciter.
Le principe de continuité ne saurait être imputé à Zarlino : il est une invention de ses détracteurs, et de ceux de l’intonation juste. C’est le principe d’alignement qui rend compte au mieux, nous croyons l’avoir montré, de la théorie de Zarlino. Répétons-le, ce que Zarlino préconise est un changement d’espèce, ni moins, ni plus : le remplacement du diatono par le sintono. Un tel changement, intervenant au sein d’un système diatonique modulaire, va modifier l’architecture interne des modules (tétracordes ou hexacordes) mais en aucun cas l’architecture générale du système. Quelle que soit l’espèce, les hexacordes continuent à se succéder à intervalles de quintes ou de quartes pures et l’architecture générale du système reste, en ce sens, pythagoricienne.
Le cristal syntonique est un système à diapason fixe. Cette fixité n’est en rien attribuable à l’imposition dans le domaine de la musique vocale d’un modèle inspiré du clavier81, mais est au contraire une caractéristique fondamentale de tous les systèmes, diatoniques, chromatiques ou enharmoniques décrits par Zarlino et ses contemporains. Le principe d’alignement conduit donc à la stabilité du diapason aussi mécaniquement que le principe de continuité conduit à sa fluctuation.
Un autre propos de Walker82 est de souligner le caractère « neutre » de l’intonation juste, à l’égard des deux versions opposées de Wibberley et de Bent. Comme les points de la texture polyphonique provoquant des conflits en matière d’intonation juste sont les enchaînements inter-hexacordaux qui s’accompagnent d’une distorsion de comma et se signalent par une fausse relation, le fait que la version Bent, comme la version Wibberley, comprennent six et seulement six de ces enchaînements les place en effet à stricte égalité vis à vis de l’intonation juste. Pourrait-on alors concevoir une réalisation qui supprime tout enchaînement inter-hexacordal et réconcilie, par là-même, le principe de continuité et le principe d’alignement ? Certainement. Il suffirait pour cela de résoudre toutes les fausses relations en ajoutant des bémols successifs.
Faisons l’exercice et ajoutons successivement Bb (soprano, troisième minime de 45), Eb (ténor, quatrième minime de 45), Ab (basse, première minime de 46), Db (ténor, quatrième minime de 46), Gb (basse et alto, début de 47), Cb (soprano, troisième minime de 47), Fb (ténor, quatrième minime de 47), Bbb (basse, début de 48), Ebb (ténor, quatrième minime de 48), Abb (basse, début de 49), Dbb (soprano, troisième minime de 49), Gbb (ténor, quatrième minime de 49), Cbb (basse et alto, début de 50), Fbb (soprano, quatrième minime de 50), Bbbb (basse, début de 51), Ebbb (soprano, quatrième minime de 51), Abbb (basse, début de 52), Dbbb, Gbbb (troisième minime de 52) et Cbbb (53). Nous avons produit une version complètement loufoque, mais qui ne pose plus aucun problème d’intonation juste parce que tous les enchaînements inter-hexacordaux entraînant des distorsions de comma ont été éliminés83. Cette version, qu’on peut s’amuser à écouter ici (Exemple 4.15) en intonation juste, se termine sur un Cbbb, soit trois apotomes plus bas qu’elle n’avait commencé, ce qui n’empêche pas, paradoxalement, le diapason de rester parfaitement stable d’un bout à l’autre de cette excursion de vingt hexacordes en direction molle.
Alors… Idéal ou utopie ? Vouloir trancher de manière catégorique à propos de tout ce qu’il est possible de ranger sous le terme d’intonation juste n’est évidemment pas adéquat. Nous jugeons préférable de dresser une liste, au moins provisoire, de ce qui, dans cette constellation théorique, fut et reste utopique. Une fois éliminée cette part d’impossible, nous distinguerons mieux ce qui a pu, au cours de l’histoire de la musique, jouer le rôle d’un idéal. Nous n’entendons pas qu’un tel idéal ait été atteint avec une précision absolue – quel système d’accord saurait-il prétendre à cela ? – mais seulement qu’il a pu, ou pourrait guider les chanteurs et influencer, de manière aussi précise que le permet la physiologie humaine, leurs comportements en matière d’intonation.
Si, par intonation juste, l’on entend que toutes les consonances, verticales, horizontales et obliques, doivent toujours être pures, alors l’intonation juste est utopique. Comme nous l’avons vu, il est des enchaînements diatoniques élémentaires qui ne peuvent remplir cette exigence. Il y aura donc toujours, dans la pratique, des situations où il faudra sacrifier une consonance au profit d’une autre.
Si, par intonation juste, l’on entend principe de continuité, alors l’intonation juste est utopique : les dérives, parfois rapides, du diapason que provoque l’application de ce principe produisent un effet insupportable pour notre oreille. Comme nous l’avons vu également, les bases historiques dudit principe sont pratiquement inexistantes à la Renaissance, et ce n’est certainement pas chez Zarlino qu’il faut aller les chercher. Le principe de continuité est à notre avis une construction rétrospective, destinée réfuter par l’absurde les affirmations de Zarlino sur l’usage des intervalles purs. En fait, ce principe ne prouve qu’une seule chose : qu’il est lui-même, et lui seul, utopique.
Si l’on exige qu’elle puisse être réalisée par des instruments à clavier, alors l’intonation juste est utopique. Une pièce donnée ne recrute le plus souvent qu’un nombre relativement limité de fréquences, mais un corpus de pièces de la Renaissance requerrait un nombre bien trop important de cordes pour qu’on puisse se contenter de quelques feintes brisées. Les touches « blanches » elles-mêmes, en priorité, devraient être divisées en deux, peut-être en trois. De tels claviers, en admettant qu’ils soient techniquement réalisables, se heurteraient à la limitation des cinq doigts de la main humaine et resteraient inutilisables.
Si l’on exige qu’elle repose sur une « gamme naturelle », c’est-à-dire une séquence diatonique couvrant l’octave, et qui en représenterait l’étalon, alors l’intonation juste est utopique. La plus grande séquence diatonique qui ne renferme que des consonances pures est le tétracorde. En pratique, un système d’hexacordes syntoniques peut, comme nous l’avons vu, servir de repère de manière fort satisfaisante. Le passage à la gamme, c’est-à-dire le remplacement des modules diatoniques par une seule séquence linéaire, entraîne une rigidification délétère du système diatonique. L’intonation juste est en fait radicalement incompatible avec la notion de gamme, et c’est peut-être pour cela qu’elle est si mal comprise aujourd’hui.
Si l’on s’attend à ce que n’importe quels chanteurs, abandonnés par les instruments, adoptent spontanément une intonation juste84, on se trouve une fois encore en pleine utopie. Zarlino lui-même, bien qu’il fasse souvent appel à la Nature pour justifier ses spéculations, n’y croit pas. Pour lui, ce n’est qu’aux esperti Cantori que la Nature enseigne à former des intervalles purs. L’intonation juste n’a donc rien, en tant que technique, de « naturel ». Elle est au contraire le fruit d’une élaboration complexe et nécessite une très grande maîtrise. La « justesse » doit faire l’objet d’un apprentissage et d’un long conditionnement qui, selon la musique pratiquée, peuvent s’appuyer sur une béquille instrumentale et s’orienter vers tel ou tel tempérament, ou bien se référer à un modèle dérivé du sintono et tendre vers l’intonation juste.
La part de l’utopie étant faite, nous pouvons maintenant rappeler sous quelle forme l’intonation juste a pu, malgré tout, fonctionner comme idéal, c’est-à-dire comme un modèle serré de près par des exécutants humains.
Au xvie siècle, de nombreux chanteurs se sont efforcés, après les Istitutioni, de produire des intervalles purs. Nous le savons, non par Zarlino mais bien par Galilei, son plus vif détracteur, ce qui donne un poids certain au témoignage. Si, pour parvenir à un tel résultat, ces chanteurs sont partis des écrits de Zarlino, c’est logiquement à un système proche de celui que nous avons décrit qu’ils ont dû parvenir. S’il a existé des chapelles qui ont pratiqué de manière totalement contrôlée ce type d’intonation, les règles explicites qu’elles employaient ont sans doute disparu avec elles. Nous postulons qu’elles menaient grosso modo à l’application de ce que nous avons appelé le principe d’alignement, et que l’alignement en question se faisait sur un repère modulaire formé d’hexacordes renfermant chacun un maximum de consonances pures. Il n’est pas exclu que la solmisation ait joué un rôle pour discriminer les cordes dédoublées, comme le donnent à penser les Sopplimenti. Voilà qui constitue une hypothèse forte sur l’usage de l’intonation juste à la Renaissance. Bien qu’elle ne soit à notre avis pas utopique, elle repose, nous devons le reconnaître, sur des indices historiques plutôt ténus.
On peut formuler aussi une hypothèse plus faible, selon laquelle ce serait à un niveau partiellement implicite que se serait fait le mariage entre le sintono et le système hexacordal. A la Renaissance, les bases de la lecture musicale s’acquéraient le plus souvent dans l’enfance, à un âge où les chanteurs n’étaient bien évidemment pas capables de comprendre les spéculations mathématiques d’un Zarlino. Imaginons que, dans quelque chapelle de bonne qualité, on soit parvenu d’une manière ou d’une autre à une intonation très pure : si, d’une part, les nouveaux chanteurs (souvent des enfants) possédaient une finesse d’oreille suffisante pour bien maîtriser la subtilité de modules diatoniques comme l’hexacorde syntonique et que, d’autre part, pour l’emplacement de leurs muances, il aient adopté par imitation les habitudes de leurs aînés, ils devaient alors, sans connaissance théorique approfondie, parvenir à intégrer et à reproduire le système d’intonation qui était en vigueur dans la chapelle en question.
Dans une hypothèse encore plus faible, les chanteurs, tout en continuant à se référer en théorie à la main guidonienne traditionnelle se seraient mis à ajuster leurs tierces et leurs sixtes. La permanence d’un repère théorique pythagoricien aurait quant à elle contribué à stabiliser le diapason. Le résultat obtenu – une intonation fondée, dans le détail, sur des consonances pures mais, globalement, sur un système d’hexacordes se succédant à distance de quintes pures – devait ressembler d’assez près à celui que donne l’application du principe d’alignement. Des faits de ce type sont fort bien attestés historiquement, aussi bien par Zarlino que par Galilei85. Les deux adversaires s’accordent en effet à reconnaître que, bien avant les Istitutioni, des générations de chanteurs ont produit tierces et sixtes pures tout en étant persuadés de rester fidèles au diatono pythagoricien.
Et au xxe siècle ? Nous ne pouvons bien sûr nous prévaloir, pour l’exécution de la musique de la Renaissance, d’aucune tradition orale. Au contraire de ce qui pouvait se passer au xvie siècle, nous ne bénéficions pas de cet apprentissage par immersion où l’oreille joue le premier rôle. Si, par conséquent, nous voulons tenter de renouer avec une pratique que nous postulons historique et dont nous pensons qu’elle a un intérêt esthétique, comme l’intonation juste, nous en serons réduits, tout au moins dans un premier temps, à élaborer de manière rationnelle et théorique un modèle de référence qui soit conforme avec les exigences de Zarlino. Dans un deuxième temps seulement , lorsque nous aurons pu traduire notre modèle en sons – ce qu’un logiciel comme Zarlino permet maintenant de réaliser aussi précisément que facilement – nous pourrons faire appel à notre oreille.
Le haut-le-cœur que nous éprouvons, occidentaux du xxe siècle, en entendant certaines dérives du diapason dont est responsable le principe de continuité, montre à tout le moins que l’application dudit principe fait violence au repère diatonique implicite qui est le nôtre. On pourrait bien sûr arguer que c’est l’éducation musicale moderne qui est responsable de ce rejet et que des oreilles renaissantes auraient été charmées par telle baisse rapide de cinq à six commas. Il n’existe à notre avis aucune base historique pour défendre sérieusement un tel point de vue. L’enseignement de la musique, fondé sur la main guidonienne, système stable entre tous, la fréquentation d’instruments de musique qui, par la force des choses, ne pouvaient détonner devaient, hier comme aujourd’hui, amener tout musicien à se constituer un repère diatonique stable. Jusqu’à preuve du contraire, nous admettons donc que la perception de l’occidental ayant bénéficié d’une éducation musicale ne s’est pas, en quelques pauvres siècles, modifiée au point que des naufrages comme ceux que nous donnons à entendre aient pu à l’époque paraître agréables, ou seulement tolérables. Le malaise qui nous prend à leur écoute est profond et n’a rien à voir avec le simple et tès vite agréable dépaysement auditif que nous éprouvons lorsque nous entendons au clavier un tempérament auquel nous ne sommes pas habitués. Ce que nous subissons évoque plutôt, si l’on recherche une analogie instrumentale, un grave défaut d’accord : un instrument désaccordé a, de toute éternité, sonné mal, et il continue de le faire de nos jours.
Le système que nous avons décrit constitue un modèle de référence fonctionnel : il conduit, par le moyen de procédures pouvant être appliquées de manière presque complètement mécanique, à une forme d’intonation juste qui « sonne » globalement bien. Il permet de débusquer facilement les distorsions de comma et de les résoudre de manière simple. Enfin, il présente l’avantage de ne pas faire intervenir de notion théorique moderne comme celles de gamme, de tonalité ou de modulation, dont l’application à la polyphonie de la Renaissance n’est pas probante. L’hexacorde syntonique, en tant que module constitutif d’un repère diatonique, peut fournir aux chanteurs désireux d’affiner leur intonation aussi bien que leur oreille un excellent terrain d’exercice.
Sans l’avoir véritablement cherché, nous venons d’être ramené au vieux débat inauguré il y a plus de deux mille ans par la querelle entre aristoxéniens et pythagoriciens, et qui porte sur la place respective à accorder, en musique, au jugement de l’oreille et à celui de la raison. C’est sur lui que Zarlino ouvre ses Istitutioni86 et c’est sur lui aussi qu’il les boucle quatre cent pages plus loin87. Sa méthode, dans la droite ligne de celle qu’avait déjà adoptée Ptolémée, coïncide assez exactement avec celle que nous impose notre position d’observateur distant de plus de quatre siècles : construire un modèle rationnel, puis le mettre à l’épreuve de l’oreille. C’est donc à Zarlino que nous laisserons le dernier mot : « Non è perciò da dar questo ufficio di giudicare al sentimento solamente nelle cose dei Suoni, et delle voci : ma li dobbiamo accompagnar sempre la Ragione. Ne meno si debbe dare tutto il giudicio alla Ragione lasciando da parte il Senso; percioche l’uno senza l’altro potrà sempre essere cagione di errore88 ».
(Utilisez la touche « retour » de votre navigateur pour revenir au texte)
Zarlino, Istitutioni harmoniche. L’ouvrage a connu plusieurs éditions, qui sont un signe de son succès. Nous nous y référons par l’abréviation Ist, suivie des deux chiffres caractérisant l’année de l’édition consultée. Le chiffre romain désigne la partie du traité concernée, et le chiffre arabe qui le suit, le chapitre.
Il s’agit d’un tempérament mésotonique aux 2/7 de comma syntonique. Ist58 II, 40-44.
HORA può nascere vn dubbio, considerato quello, ch’io hò detto di sopra, Se tra le parti delle Canzoni, o cantilene, le cui harmonie nascono da gli istrumenti naturali, si odono i veri, & legitimi interualli contenuti nelle loro vere forme, o pure li accresciuti, o diminuti, secondo il modo mostrato. Al qual dubbio si può rispondere, & dire, che veramente si odono quelli, che sono contenuti nelle lor forme vere, & non gli altri: Ist58 II,45.
Il a bien sûr lui-même des précurseurs, au nombre desquels on cite habituellement W. Odington, B. Ramos, P. Aaron., L. Fogliano etc.
Faute d’un meilleur terme, nous nous tiendrons à cette appellation et nous passerons dorénavant des guillemets.
L’emploi de nombreux conditionnels vient renforcer cette impression : Ma quando le Voci fussero tra loro proportionate, & bene vnite, senza hauere alcuno impedimento; & fossero proferite da i Cantori con qualche discrettione, & con buon giudicio; di maniera che l’vna voce non superasse l’altra; io tengo per fermo, che tali interualli si vdirebbeno perfetti; & che gli vditori piglierebbeno non poco piacere, & contento delle cantilene, che vdissero: Ist58 II,45.
Voir en particulier les travaux de Barbieri, Lindley, Haynes.
Vicenzo Galilei, Dialogo, ci après Dial.
Haynes, Beyond temperament, p. 359.
Quella (spezie) dove concorrono universalmente tutti i prattici de’ tempi nostri, mossi dall’autorità del Reverendo M. Gioseffo Zarlino. Dial, p.2 :
Hermann von Hemholtz, Théorie physiologique de la musique, p. 421-2.
Théorie physiologique, p. 430.
Théorie physiologique, p. 364.
C’est par simple convention que nous adoptons cette terminologie.
Théorie physiologique, p. 368.
Pour une introduction détaillée au système pythagoricien, voir Margo Shulter, Pythagorean Tuning. Dès maintenant, nous adoptons une notation en lettres pour le « nom » des notes (C - D - E -F -G -A -B correspondent donc à do-ré-mi-fa-sol-la-si du solfège qui a prévalu dans les pays latins), b et # désignent respectivement le bémol et le dièse, le nombre de dièses ou de bémols pouvant altérer une note n’étant bien sûr pas limité. Nous réservons les syllabes ut-ré-mi-fa-sol-la au domaine de la solmisation hexacordale.
James Murray Barbour, Tuning and Temperament, p. vi-vii.
Pierre-Yves Asselin, Musique et tempérament, p. 62.
Dominique Devie, Le Tempérament musical, p. 41.
C’est néanmoins sur le labyrinthe de Barbour que se fonde le logiciel Zarlino, avant tout parce que ce système est exhaustif. Dégagé des contraintes matérielles du clavier, l’ordinateur calcule et joue avec une facilité déconcertante n’importe laquelle des fréquences du labyrinthe.
Barbour, Just intonation confuted, pp.50-51.
Par diapason, nous entendons la hauteur absolue à laquelle une pièce de musique est jouée ou chantée, déterminée par la fréquence d’une note de référence, par convention A.
Les deux mesures en question y sont répétées quatre fois, le tout se terminant par un accord de G majeur suivi, après un silence, par le G majeur initial.
Indeed, the better in tune a performance sounds in terms of its local progressions (with pure thirds and fifths), the more likely it is to move down, as several professional performers confirm. Margaret Bent, Diatonic ficta revisited, §13.
INTRAVIENE nella Musica quello, che suole intrauenire in alcuna dell’altre scienze: conciosiache diuidendosi in due parti, l’vna Theorica, o Speculatiua, & l’altra Prattica vien detta. Quella il cui fine consiste nella cognitione solamente della verità delle cose intese dall’intelletto (il che è propio di ciascuna scienza) è detta Speculatiua; l’altra che dall’essercitio solamente dipende, vien nominata Prattica. Ist58 I, 11.
Ist58 II, 1.
Plus qu’à un boyau tendu, le terme de corde renvoie dans la théorie à la notion abstraite d’une longueur (ou, pour nous, d’une fréquence), grandeur chiffrable pouvant être comparée à d’autres grandeurs du même type. C’est dans ce sens abstrait que nous l’utilisons.
Ist58 II, 16.
Die Harmonielehre des Klaudios Ptolemaios, p. 44, ou The Harmonics, p. 310.
Il Diatono era quello, che procedeua nelli suoi Tetrachordi per l’interuallo di vn minor Semituono, contenuto dalla proportione super 13. partiente 243. chiamato da i Greci apotomè; ancorache (come mostra Boetio) ogni spacio di Semituono chiamassero leimma, ouer diesis; & per due interualli di Sesquiottaua proportione, i quali nominarono Tuoni. Ist58 II, 16.
Unité très couramment utilisée, le cent correspond à un centième de demi-ton tempéré, sur une échelle logarithmique. On passe d’un rapport de fréquences r à un intervalle i en cents au moyen de la formule : i = log r / log 2 * 1200, où log figure un logarithme de base quelconque.
Il Sintono, ouero Incitato, che lo vogliamo dire, era quello, del quale il suo Tetrachordo procedeua dal graue uerso l’acuto per vno interuallo, contenuto tra la sua prima chorda graue, & la seconda, dalla Sesquiquintadecima proportione; & per vno di Sesquiottaua, posto tra la seconda & la terza, & per vno contenuto dalla Sesquinona, posto tra la terza & la quarta chorda acuta: Et per il contrario discendendo dall’acuto al graue, procedendo per gli istessi interualli; come si vede. Et questo è quello, che vsano i Moderni nelle loro Harmonie: conciosia che i termini delle sue proportioni sono collocati tra i Numeri Sonori, come nel cap. 15. della Prima parte si può vedere. Ist58 II,16.
Ist58 II, 28. Pour les termes grecs, nous reprenons telles quelles les traductions et translittérations de Zarlino.
Ist58 II, 28.
La plus petite valeur du proslambanomenos qui permettrait d’attribuer un nombre entier à chaque corde serait 4608, soit 9216/2.
SE NOI vorremo essaminar la mostrata diuisione, ouero ordinatione, non è dubbio, che ritrouaremo in lei vna grande imperfettione: conciosia che è priua di quelli interualli, che da tutti li Musici di commun parere sono accettati al presente per consonanti, & sono quelli del Semiditono, del Ditono, & li composti, i quali nelle loro compositioni continouamente si odono. Ist58 II, 31.
Ist58 II, 40.
Ist58 II, 30.
C’est lui en effet qui, le premier, proposa, à titre didactique, de représenter ce système sur les articulations d’une main. Les pédagogues se tinrent à cette méthode durant des siècles.
Par cela, nous entendons seulement que le la d’un hexacorde naturel correspond toujours à une clef A, ce qui ne signifie pas, bien sûr, que aa soit standardisé à 440 Hz.
De bas en haut, on avait donc Gamma ut, A ré, B mi, C fa-ut, D sol-ré, E la-mi, F fa-ut, G sol-ré-ut, a la-mi-ré, b fa-b(carré) mi, c sol-fa-ut, d la-sol-ré, e la-mi, f fa-ut, g sol-ré-ut, aa la-mi-ré, bb-fa bb(carré) mi, cc sol-fa, dd la-sol, ee la.
Pour un exposé des rudiments de la méthode de Gui d’Arezzo, on se référera avec profit à l’article de P. Drummond, Solmization, New Grove Dictionnary of Music and Musicians, 1988, vol. 17, p. 458-462.
Ist58 II, 48 et II, 39.
Karol Berger, Musica ficta, p. 29-48, s’est attaché à montrer, à partir d’un examen approfondi des sources, que la théorie de la musica ficta ne permet l’ajout que d’un nombre limité d’hexacordes. Selon lui, il n’était pas pensable, au Moyen Âge et à la Renaissance, de dépasser A# en direction dure ni Gb en direction molle. Margaret Bent, quant à elle, présente (Diatonic ficta) des exemples pratiques où l’application des règles d’évitement du triton semble entraîner un dépassement de ces limites. Nous n’entendons pas prendre position dans ce débat. Nous préférons seulement, à des fins de démonstration, considérer le système d’imbrication des hexacordes comme théoriquement illimité, quitte à admettre que les praticiens de la Renaissance devaient bien s’imposer certaines limites en la matière.
Sop IV, 6.
Un cas célèbre, Le Kyrie Libenter gloriabor d’Obrecht, a été abondamment discuté, en particulier par Margaret Bent, Diatonic ficta, p. 34 et sq. Notre propos n’est pas d’accepter ou de contester la version « spiralée » que l’auteur propose, mais simplement de relever que, même avec sept muances successives en direction molle, elle reste inscrite au sein d’un système à diapason fixe. Le fait que, dans la notation originale, une telle excursion ne soit pas signalée, alors qu’elle se traduit par des bémols et même des doubles bémols dans la notation moderne, est à cet égard accessoire.
Cf. par exemple Berger, Musica ficta, p. 94, 116.
Berger, Musica ficta, p. 144.
Si l’on raisonne en termes de solmisation, on voit que le A du ténor, qui est le mi d’un hexacorde dur, ne peut pas former une sixte pure avec un autre mi puisque tous les mi appartiennent à la même série de quintes. De même, ré et mi étant deux voix abaissées, la tierce ré-mi apparaissant entre l’alto et le soprano ne saurait être pure.
Par ce terme, il peut désigner des compositeurs, mais tout aussi bien des praticiens du contrepoint, c’est-à-dire des chanteurs annotant leur partie.
… di qui hanno tolto forse occasione alcuni de’ moderni Contrapuntisti, di segnare il b quadro in F faut, quando elle ha hauuto à rispondere per Quinta con h mi, & il diesis X, quando con D solre ha fatto Terza maggiore, ò la sua replicata con d la sol re : argumentando tacitamente, che la Quinta non verrebbe giusta con il diesis X come col h quadro ; ma vn poco scarsa & rimessa : Dial p.26.
Il s’agit bien d’un f-mi, donc d’un F élevé d’un demi-ton et non d’un F naturel au sens moderne du terme.
Ist58 II,38 et 46.
Sop IV,11.
Ist58, II,31.
Dial p.12.
Et ben che lo intervallo del Comma non sia adoperabile in alcun genere : non è però nato senza utile : conciosia che col suo mezo si viene all acquisto di molte consonanze. Ist58 II,40. Cf. aussi Ist58 III,17.
Conciosia che questo intervallo [le comma] nelle Voci, che per loro natura in ogni parte si piegano si accomoda de maniera che non si ode. Ist58 II,40. Cf. aussi Sop IV,6.
Ist58 II,45.
Dial pp.1-39.
Dial pp.33.
Ist58 II,41-44. On trouve une description moderne de ce tempérament chez Barbour, Tuning and Temperament, p.33 et chez Asselin, Musique et tempérament, pp.85-87. Devie, Le Tempérament musical, émet des doutes quant à son utilisation pratique.
Dial pp.43-47.
Dial pp.30 et 54.
Ist58, Proemio.
Nous nous basons pour cela sur notre hexacorde syntonique, de séquence t-T-S-T-t. En partant d’une autre séquence, on aboutirait à des résultats quelque peu différents. C’est néanmoins la séquence ci-dessus qui produit les résultats les plus directement utilisables.
La terminologie étant en la matière un peu flottante, nous précisons ici notre acception. Nous parlons de fausse relation lorsque deux notes constituant une consonance parfaite (unisson, quarte, quinte ou octave) diminuée ou augmentée se trouvent à proximité directe l’une de l’autre. Lorsque ces deux notes se font entendre simultanément pour une partie au moins de leur durée, nous parlons de fausse relation verticale. Lorsqu’elles surviennent successivement dans la même voix, nous parlons de fausse relation horizontale, et de fausse relation oblique lorsqu’elles surviennent successivement entre deux voix différentes.
Ist58 III, 30.
Il semble en particulier s’y appliquer dans le motet Ecce iam venit plenitudo.
Roger Wibberley, Josquin’s Ave Maria.
Jonathan Walker, Intonational injustice.
La présence de sixtes fait que la note de base du triplet n’est pas le F de la basse mais bien le D du ténor.
Nous considérons le E au ténor de la fin de la mesure 48 comme dissonant et nous basons donc le triplet sur G).
Nous négligeons les croches L et F à l’alto et au ténor, qui sont des notes de passage.
Nicolas Meeus (MTO-talk, 19 août 1996) a calculé une chute de cinq commas seulement, mais il s’arrête au début de la mesure 52 et ne prend donc pas en compte le dernier enchaînement inter-hexacordal.
Si l’on se place dans la perspective de chanteurs bien au fait de la solmisation et des règles d’évitement des fausses relations, qui exécuteraient l’Ave Maria de Josquin sur des parties séparées, et donc sans bénéficier d’une édition moderne en partition, on n’a pas de peine à admettre qu’ils puissent éventuellement aboutir, au cours d’une répétition, à une version proche de celle de M. Bent. Une telle version nous paraît toutefois relativement peu probable, non pas que nous partagions l’argumentation « modale » de Wibberley, mais plutôt parce que nous doutons qu’une « petite » cause comme la brève rencontre d’un Bb et d’un E à la fin de la mesure 48 soit suffisante pour entraîner un « grand » effet comme le déplacement du chant d’un long passage de plusieurs hexacordes en direction molle, avec un retour particulièrement abrupt dans le chant dur pour les deux derniers accords (à cet égard, nous nous sentons proche de l’argumentation développée par Peter Urquhart). Reste à savoir s’il serait raisonnable, de la part d’un éditeur, d’anticiper le comportement des chanteurs au point de noter la cascade de bémols suggérés par M. Bent, plutôt que de laisser chaque groupe d’interprètes parvenir à sa version propre.
Walker, Intonational injustice, I.6, I.9.
Walker, Intonational injustice, Abstract.
Walker, Intonational injustice, Abstract.
Walker, Intonational injustice, I.6
Nous faisons bien sûr abstraction de quelques notes de passage. Il subsiste en fait un enchaînement inter-hexacordal de type MU, sans distorsion de comma. Nous laissons le soin au lecteur de le débusquer, de même que d’autres qui auraient pu nous échapper.
Cette attitude apparaît de manière particulièrement nette chez N. L. Norden, A New Theory.
Ist58 I,1.
Ist58 IV,36.
Ist58 IV,36.